题目内容
平面直角坐标系中,原点到直线y=kx+b的距离公式为d=| |b| | ||
|
(1)原点到直线y=-
| 4 |
| 3 |
(2)若原点到y=(1-k)x+2k的距离为该直线与y轴交点到原点距离的一半,则k=
(3)若(1)中的直线与y轴、x轴交于A、B两点,直线AC与x轴交于C点,若∠ABC的邻补角是∠ACB的邻补角的2倍,求原点到直线AC的距离.
分析:(1)由题意,b=4,k=-
,代入公式,解答出即可;
(2)由题意,该直线与y轴交点到原点距离的一半,即当x=0时,y=2k的一半,所以
=|k|,解答出即可;
(3)作∠ABG的平分线BH,过A作AC′∥BH,根据边角关系可得出OC′的长,则可得出OC的长,进而求出直线AC的解析式,代入公式即可求出距离.
| 4 |
| 3 |
(2)由题意,该直线与y轴交点到原点距离的一半,即当x=0时,y=2k的一半,所以
| |2k| | ||
|
(3)作∠ABG的平分线BH,过A作AC′∥BH,根据边角关系可得出OC′的长,则可得出OC的长,进而求出直线AC的解析式,代入公式即可求出距离.
解答:解:(1)∵b=4,k=-
,
∴d=
=
;
(2)根据题意得,
=|k|,
解得k=1±
;
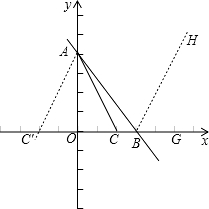
(3)由题意得,点A(0,4),B(3,0),则AB=5,
如图,∵∠ABC的邻补角是∠ACB的邻补角的2倍,
∴点C只能在线段OB上,2∠ACO=∠ABG,
作∠ABG的平分线BH,过A作AC′∥BH,
∴∠AC′C=∠HBG=∠ABH=∠C′AB=∠ACO,
∴BC′=AB=5,由OB=3,
∴OC′=2,
∵∠AC′C=∠ACO,
∴AC′=AC,又AO⊥CC′,
∴OC=OC′=2,
∴C(2,0),
∴直线AC的解析式为y=-2x+4,
∴d=
=
.
| 4 |
| 3 |
∴d=
| 4 | ||||
|
| 12 |
| 5 |
(2)根据题意得,
| |2k| | ||
|
解得k=1±
| 3 |

(3)由题意得,点A(0,4),B(3,0),则AB=5,
如图,∵∠ABC的邻补角是∠ACB的邻补角的2倍,
∴点C只能在线段OB上,2∠ACO=∠ABG,
作∠ABG的平分线BH,过A作AC′∥BH,
∴∠AC′C=∠HBG=∠ABH=∠C′AB=∠ACO,
∴BC′=AB=5,由OB=3,
∴OC′=2,
∵∠AC′C=∠ACO,
∴AC′=AC,又AO⊥CC′,
∴OC=OC′=2,
∴C(2,0),
∴直线AC的解析式为y=-2x+4,
∴d=
| |4| | ||
|
4
| ||
| 5 |
点评:本题主要考查了一次函数综合题,点到直线的距离等知识,(3)小题中,作辅助线根据边角关系得出OC的长,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)在平面直角坐标系中,描出下列各点:(0,0)、(1,2)、(1,0)、(2,2)、(2,0),并用线段顺次连接各点,你得到了怎样的图案?若各点纵坐标不变,横坐标分别乘以-1,所得的图形与原图形有什么变化?
(1)在平面直角坐标系中,描出下列各点:(0,0)、(1,2)、(1,0)、(2,2)、(2,0),并用线段顺次连接各点,你得到了怎样的图案?若各点纵坐标不变,横坐标分别乘以-1,所得的图形与原图形有什么变化? 如图,在平面直角坐标系中,将凹四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(l,3),C(3,3),D(3,1).
如图,在平面直角坐标系中,将凹四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(l,3),C(3,3),D(3,1).