题目内容
(2007•湘潭)如图1,设抛物线y= x2-
x2- 交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.
交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.(1)求抛物线的对称轴;
(2)将△ACB绕圆心M顺时针旋转180°,得到三角形APB,如图2.求点P的坐标;
(3)有一动点Q在线段AB上运动,△QCD的周长在不断变化时是否存在最小值?若存在,求点Q的坐标;若不存在,说明理由.

【答案】分析:(1)根据抛物线的对称轴公式即可得出所求的结果.
(2)可先根据抛物线的解析式求出A、B、C三点的坐标,过P作PE⊥x轴于E,根据旋转的性质不难得出BE=OA,PE=OC,由此可求出P点的坐标.
(3)本题的关键是找出Q点的位置,取C关于x轴的对称点C′,连接C′D与x轴的交点就是Q点.可先求出直线C′D的函数解析式,进而可得出Q点的坐标.
解答: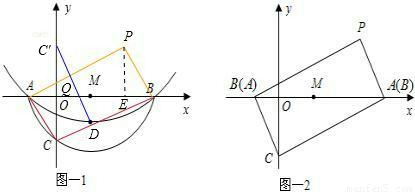 解:(1)由题意可知:抛物线的对称轴为x=1.
解:(1)由题意可知:抛物线的对称轴为x=1.
(2)过P作PE⊥x轴于E,则有△PEB≌△OAC
易知A(-1,0)、B(3,0)、
C(0,-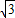 ).
).
∴OA=BE=1,OB=AE=3,EP=OC=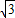
∴OE=OB-BE=2
即P点坐标为(2,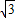 ).
).
(3)设C关于x轴的对称点为C′(0,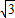 ),
),
已知抛物线顶点D(1,-1).
设直线C′D的解析式为y=kx+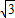 ,则有:
,则有:
k+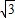 =-1,k=-1-
=-1,k=-1-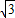
因此直线CD的解析式为y=(-1-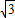 )x+
)x+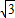 .
.
令y=0,则x=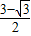
∴Q点坐标为(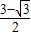 ,0).
,0).
点评:本题主要考查了二次函数的性质、全等三角形的判定和性质等知识点,(3)题找出Q点的位置是解题的关键.
(2)可先根据抛物线的解析式求出A、B、C三点的坐标,过P作PE⊥x轴于E,根据旋转的性质不难得出BE=OA,PE=OC,由此可求出P点的坐标.
(3)本题的关键是找出Q点的位置,取C关于x轴的对称点C′,连接C′D与x轴的交点就是Q点.可先求出直线C′D的函数解析式,进而可得出Q点的坐标.
解答:
 解:(1)由题意可知:抛物线的对称轴为x=1.
解:(1)由题意可知:抛物线的对称轴为x=1.(2)过P作PE⊥x轴于E,则有△PEB≌△OAC
易知A(-1,0)、B(3,0)、
C(0,-
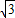 ).
).∴OA=BE=1,OB=AE=3,EP=OC=
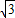
∴OE=OB-BE=2
即P点坐标为(2,
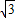 ).
).(3)设C关于x轴的对称点为C′(0,
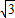 ),
),已知抛物线顶点D(1,-1).
设直线C′D的解析式为y=kx+
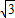 ,则有:
,则有:k+
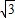 =-1,k=-1-
=-1,k=-1-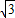
因此直线CD的解析式为y=(-1-
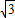 )x+
)x+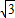 .
.令y=0,则x=
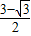
∴Q点坐标为(
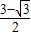 ,0).
,0).点评:本题主要考查了二次函数的性质、全等三角形的判定和性质等知识点,(3)题找出Q点的位置是解题的关键.

练习册系列答案
相关题目
 x2-
x2- 交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.
交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.
 x2-
x2- 交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.
交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.