题目内容
已知等腰梯形的高为5cm，两底之差为10cm，则它的锐角为________度．
45
分析：作AE⊥BC、DF⊥BC，根据等腰梯形的性质可推得△ABE≌△DCF，从而得到BE=CF，又因为AEFD为矩形，则AD=EF，因此BE=FC=（BC-AD）÷2=5，而AE=DF=5cm，所以△ABE、△DCF为等腰直角三角形，则∠B=∠C=45°．
解答：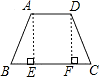
解：如图，作AE⊥BC、DF⊥BC，BC-AD=10cm，AE=DF=5cm
∵四边形ABCD等腰梯形
∴AB=DC，∠ABE=∠DCF，AE=DF
∴△ABE≌△DCF
∴BE=CF
∵BC-AD=10cm，AD=EF
∴BE+FC=10cm
∴BE=FC=5cm
∵AE=5cm
∴△ABE、△DCF为等腰直角三角形
∴∠B=∠C=45°
点评：本题主要考查等腰梯形的性质的应用．
分析：作AE⊥BC、DF⊥BC，根据等腰梯形的性质可推得△ABE≌△DCF，从而得到BE=CF，又因为AEFD为矩形，则AD=EF，因此BE=FC=（BC-AD）÷2=5，而AE=DF=5cm，所以△ABE、△DCF为等腰直角三角形，则∠B=∠C=45°．
解答：
解：如图，作AE⊥BC、DF⊥BC，BC-AD=10cm，AE=DF=5cm∵四边形ABCD等腰梯形
∴AB=DC，∠ABE=∠DCF，AE=DF
∴△ABE≌△DCF
∴BE=CF
∵BC-AD=10cm，AD=EF
∴BE+FC=10cm
∴BE=FC=5cm
∵AE=5cm
∴△ABE、△DCF为等腰直角三角形
∴∠B=∠C=45°
点评：本题主要考查等腰梯形的性质的应用．
练习册系列答案
名校课堂系列答案
相关题目