题目内容
【题目】【观察发现】
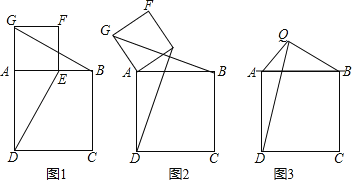
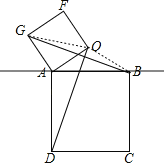
如图1,四边形ABCD和四边形AEFG都是正方形,且点E在边AB上,连接DE和BG,猜想线段DE与BG的数量关系,以及直线DE与直线BG的位置关系.(只要求写出结论,不必说出理由)
【深入探究】
如图2,将图1中正方形AEFG绕点A逆时针旋转一定的角度,其他条件与观察发现中的条件相同,观察发现中的结论是否还成立?请根据图2加以说明.
【拓展应用】
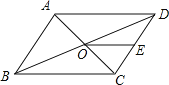
如图3,直线l上有两个动点A、B,直线l外有一点O,连接OA,OB,OA,OB长分别为![]() 、4,以线段AB为边在l的另一侧作正方形ABCD,连接OD.随着动点A、B的移动,线段OD的长也会发生变化,在变化过程中,线段OD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
、4,以线段AB为边在l的另一侧作正方形ABCD,连接OD.随着动点A、B的移动,线段OD的长也会发生变化,在变化过程中,线段OD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
【答案】【观察发现】DE=BG,DE⊥BG;【深入探究】仍然成立,理由见解析;【拓展应用】最大值为8;
【解析】
试题分析:(1)根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;
(2)结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论;
(3)以OA为边做正方形OAGF,连接OG、BG,则OC=![]() OA=4,当G、O、B三点共线时,BG最长,此时BG=OC+OB=4+4=8,从而确定正确的答案.
OA=4,当G、O、B三点共线时,BG最长,此时BG=OC+OB=4+4=8,从而确定正确的答案.
解:【观察发现】:DE=BG,DE⊥BG;
【深入探究】:【观察发现】中的结论仍然成立,即DE=BG,DE⊥BG;
理由:∵四边形ABCD、四边形CEFG都是正方形,
∴BA=AD,AG=AE,∠BAD=∠EAG=90°,
∴∠BAG=∠DAE(1分),
∵在△BAG与△DAE中,
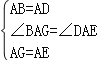 ,
,
∴△BAG≌△DAE(SAS),
∴BG=DE,∠ABG=∠ADE,
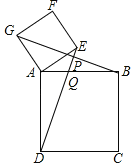
设线段DE分别与BG、AB相交于点P、Q两点,
由∠BAD=90°得∠ADE+∠AQD=90°,
∴∠ABG+∠PQB=90°,
∴∠BPQ=90°,
即DE⊥BG;
【拓展应用】以OA为边做正方形OAGF,连接OG、BG,则OG=![]() OA=4,
OA=4,
由【深入探究】可得OD=BG,
当G、O、B三点共线时,BG最长,此时BG=OG+OB=4+4=8,
即线段OD长的最大值为8.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案