题目内容
如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
,则a的值是( )
A. | B. | C. | D. |
A.
解析试题分析:过P点作PE⊥AB于E,连接PA并延长PA交x轴于点C.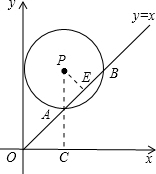
∵PE⊥AB,AB=2∴AE= AB=1,
AB=1,
∵PA=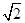 ,
,
在Rt△PAE中,由勾股定理得:PE=1,
∴PE=AE,∴∠PAE=45°,
∵函数y=x的图象与y轴的夹角为45°,
∴y轴∥PA,∴∠PCO=90°,
∴A点的横坐标为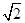 ,
,
∵A点在直线y=x上,
∴A点的纵坐标为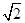 ,
,
∴PC=2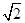 ,
,
∴a=2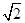 .
.
故选A.
考点: 1.切线的判定;2.一次函数图象上点的坐标特征;3.勾股定理;4.垂径定理.

练习册系列答案
相关题目
一次函数 的图象如图所示,当
的图象如图所示,当 <0时,
<0时, 的取值范围是( )
的取值范围是( )
A. <0 <0 | B. >0 >0 | C. <2 <2 | D. >2 >2 |
一条直线y=kx+b,其中k+b=-5、kb=6,那么该直线经过( )
| A.第二、四象限 |
| B.第一、二、三象限 |
| C.第一、三象限 |
| D.第二、三、四象限 |
两直线l1:y=2x-1,l2:y=x+1的交点坐标为( )
| A.(-2,3) | B.(2,-3) |
| C.(-2,-3) | D.(2,3) |
 千克,付款金额
千克,付款金额 为元,则
为元,则
 的图象如图所示,下列结论正确的是
的图象如图所示,下列结论正确的是
 ,直线
,直线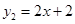 ,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.
,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.
 或
或 .
. 在同一坐标系数中的大致图象是( )
在同一坐标系数中的大致图象是( ) B
B C
C  D
D 
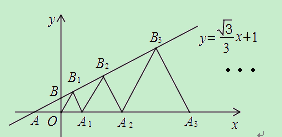
 x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )
x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )