Question

下列四组图形中，不一定相似的是（　　）

A．两直角边之比为1：2的两个直角三角形

B．任意两个等边三角形

C．有一锐角相等的两个直角三角形

D．有一个角相等的两个等腰三角形

Answer 1

分析：A、由两直角三角形的直角边之比都为1：2，再加上夹角为直角，根据两边对应成比例且夹角相等的两三角形相似可得出两直角三角形相似，不合题意；
B、任意的两个等边三角形有两对对应角相等，故相似，不合题意；
C、由一对锐角相等，加上一对直角相等，利用两对对应角相等的两三角形相似可得出两直角三角形相似，不合题意；
D、两个等腰三角形有一对角相等，可能一个为顶角，一个为底角，如图所示，故两三角形不一定相似，符合题意．

解答：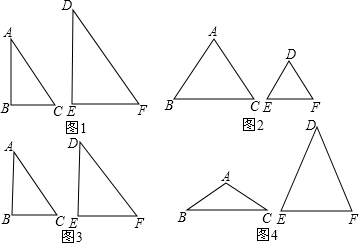
解：A、∵

AB

BC

=

1

2

，

DE

EF

=

1

2

，
∴

AB

BC

=

DE

EF

，即

AB

DE

=

BC

EF

，又∠B=∠E=90°，
∴△ABC∽△DEF，不合题意；
B、∵△ABC与△DEF都为等边三角形，
∴∠A=∠D=60°，∠B=∠E=60°，
∴△ABC∽△DEF，不合题意；
C、∵∠A=∠D，∠B=∠E=90°，
∴△ABC∽△DEF，不合题意；
D、∵AB=AC，DE=DF，
∴当∠B=∠D=30°时，∠A=120°，∠E=∠F=75°，
此时△ABC与△DEF不相似，符合题意，
故选D．

点评：此题考查了相似三角形的判定，相似三角形的判定方法有：两对对应角相等的两三角形相似；两对对应边成比例且夹角相等的两三角形相似；三对对应边成比例的两三角形相似，学生做题注意要说明一个命题为真命题必须经过严格证明，要说明一个命题为假命题，只需要举一个反例即可．