题目内容
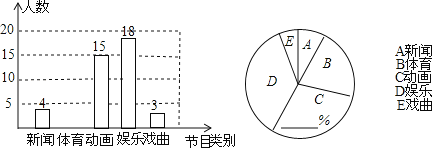
【题目】某校为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取了本校部分学生进行问卷调查(必选且只选一类节目),将调查结果进行整理后,绘制了如下不完整的条形统计图和扇形统计图,其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的3倍还多1人.
请根据所给信息解答下列问题:
(1)求本次抽取的学生人数.
(2)补全条形图,在扇形统计图中的横线上填上正确的数值,并直接写出“体育”对应的扇形圆心角的度数.
(3)该校有3000名学生,求该校喜爱娱乐节目的学生大约有多少人?
【答案】解:(1)由条形图可知,喜爱戏曲节目的学生有3人,
∵喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的3倍还多1人,
∴喜爱体育节目的学生有:3×3+1=10人,
∴本次抽取的学生有:4+10+15+18+3=50人。
(2)喜爱C类电视节目的百分比为:![]() ×100%=30%,
×100%=30%,
“体育”对应的扇形圆心角的度数为:360°×![]() =72°。
=72°。
补全统计图如下:
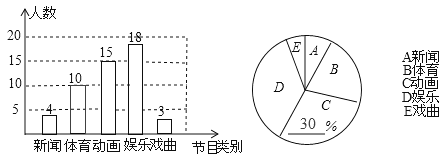
(3)∵喜爱娱乐节目的百分比为:![]() ×100%=36%,
×100%=36%,
∴该校3000名学生中喜爱娱乐节目的学生有:3000×36%=1080人。
【解析】
试题(1)先求出喜爱体育节目的学生人数,再将喜爱五类电视节目的人数相加,即可得出本次抽取的学生人数。
(2)由(1)中求出的喜爱体育节目的学生人数可补全条形图;用喜爱C类电视节目的人数除以总人数,可得喜爱C类电视节目的百分比,从而将扇形图补全;用360°乘以“体育”对应的百分比,可得“体育”对应的扇形圆
心角的度数。
(3)利用样本估计总体的思想,用3000乘以样本中喜爱娱乐节目的百分比即可得出该校3000名学生中喜爱娱乐节目的学生人数。

【题目】电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
获得好评的电影部数 | 56 | 10 | 45 | 50 | 160 | 51 |
(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率:
(2)电影公司为增加投资回报,需在调查前根据经验预估每类电影的好评率(好评率是指:一类电影中获得好评的部数与该类电影的部数的比值),如表所示:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
预估好评率 | 0.5 | 0.2 | 0.15 | 0.15 | 0.4 | 0.3 |
定义统计最![]() 其中
其中![]() 为第i类电影的实际好评率,
为第i类电影的实际好评率,![]() 为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。
为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。