题目内容
已知,a2+3a-1=0,b4-3b2-1=0,且1-ab2≠0,则(| ab2+b2+1 | a |
分析:根据已知两式求出a与b2的关系,然后代入代数式计算.
解答:解:将a2+3a-1=0,b4-3b2-1=0两式相减得:a2-b4+3a+3b2=0,
a2-b4+3a+3b2=(a2-b4)+(3a+3b2)=(a+b2)(a-b2)+3(a+b2)=(a+b2)(a-b2+3)=0,
若a-b2+3=0,则1-ab2=1-a(a+3)=-(a2+3a-1)=0,而已知1-ab2≠0,所以a+b2+3=0不成立,
则a+b2=0
∴a=-b2,
将a=-b2代入代数式
=
=
=
=2.
则(
)5=25=32.
故本题答案为:32.
a2-b4+3a+3b2=(a2-b4)+(3a+3b2)=(a+b2)(a-b2)+3(a+b2)=(a+b2)(a-b2+3)=0,
若a-b2+3=0,则1-ab2=1-a(a+3)=-(a2+3a-1)=0,而已知1-ab2≠0,所以a+b2+3=0不成立,
则a+b2=0
∴a=-b2,
将a=-b2代入代数式
| ab2+ b2+1 |
| a |
| -a2-a+1 |
| a |
| 3a-1-a+1 |
| a |
| 2a |
| a |
则(
| ab2+b2+1 |
| a |
故本题答案为:32.
点评:本题的解题关键是求出a与b2的关系,然后把代数式化简成为常数即可求值.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
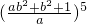 的值为________.
的值为________.