题目内容
已知
是整数，
能被3整除，求证：
和
都能被3整除．(用反证法证明)
是整数，能被3整除，求证：和都能被3整除．(用反证法证明)见解析
证明：如果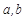
不都能被3整除，那么有如下两种情况：
（1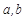）两数中恰有一个能被3整除，
不妨设能被3整除，不能被3整除，
令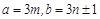
（
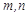都是整数），
于是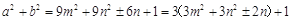
，
不能被3整除，与已知矛盾.
（2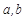）两数都不能被3整除，令
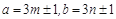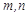（都是整数），则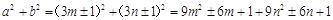
，
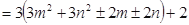不能被3整除，与已知矛盾.
由此可知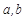，都是3的倍数．
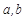不都能被3整除，那么有如下两种情况：（1）
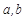两数中恰有一个能被3整除，不妨设
能被3整除，不能被3整除，令
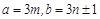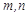（都是整数），于是
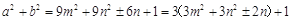，不能被3整除，与已知矛盾.
（2）
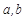两数都不能被3整除，令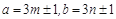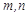（都是整数），则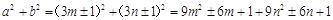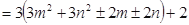，不能被3整除，与已知矛盾.
由此可知，
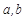都是3的倍数．
练习册系列答案
相关题目
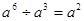
千克，不加工直接出售每千克可卖
元；如果经过加工质量减少了
，价格增加了
，
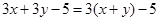
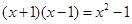
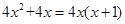
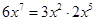
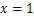时，代数式
的值为
，则当
时，代数式
与
的和是单项式，则
=_________.
元
元
元
元