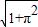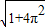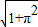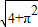题目内容
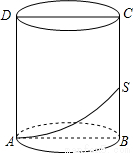
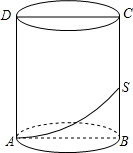 如图,圆柱形玻璃器皿的轴截面ABCD是边长为4的正方形,一只蜘蛛在容器内底部的A点,一只苍蝇停在容器内BC的中点S处,蜘蛛若想吃到苍蝇,则它移动的最短距离是
如图,圆柱形玻璃器皿的轴截面ABCD是边长为4的正方形,一只蜘蛛在容器内底部的A点,一只苍蝇停在容器内BC的中点S处,蜘蛛若想吃到苍蝇,则它移动的最短距离是
- A.2
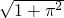
- B.2
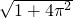
- C.4
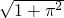
- D.2
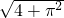
A
分析:将圆柱形容器展开,得到长为地面圆半径的一半,高为4的长方形,连接AS构造直角三角形,利用勾股定理求出AS的长即为所求.
解答: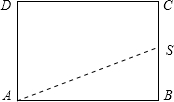 解:将圆柱展开得到如图矩形,
解:将圆柱展开得到如图矩形,
∵底面圆直径为4,
∴AB= ×4π=2π,
×4π=2π,
∵S为BC的中点,
∴BS= ×4=2,
×4=2,
∴AS=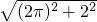 =2
=2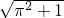 .
.
故选A.
点评:本题考查了平面展开-最短路径问题,一般要根据两点之间线段最短,将路径转化为勾股定理问题解答.
分析:将圆柱形容器展开,得到长为地面圆半径的一半,高为4的长方形,连接AS构造直角三角形,利用勾股定理求出AS的长即为所求.
解答:
 解:将圆柱展开得到如图矩形,
解:将圆柱展开得到如图矩形,∵底面圆直径为4,
∴AB=
 ×4π=2π,
×4π=2π,∵S为BC的中点,
∴BS=
 ×4=2,
×4=2,∴AS=
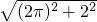 =2
=2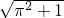 .
.故选A.
点评:本题考查了平面展开-最短路径问题,一般要根据两点之间线段最短,将路径转化为勾股定理问题解答.

练习册系列答案
相关题目
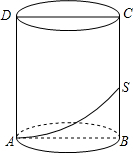 如图,圆柱形玻璃器皿的轴截面ABCD是边长为4的正方形,一只蜘蛛在容器内底部的A点,一只苍蝇停在容器内BC的中点S处,蜘蛛若想吃到苍蝇,则它移动的最短距离是( )
如图,圆柱形玻璃器皿的轴截面ABCD是边长为4的正方形,一只蜘蛛在容器内底部的A点,一只苍蝇停在容器内BC的中点S处,蜘蛛若想吃到苍蝇,则它移动的最短距离是( )