题目内容
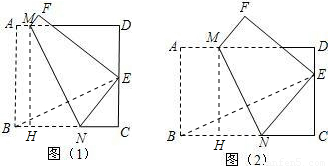
(2009•太原)问题解决:如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.当
 时,求
时,求 的值.
的值.类比归纳:
在图(1)中,若
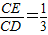 ,则
,则 的值等于______;若
的值等于______;若 ,则
,则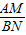 的值等于______;若
的值等于______;若 (n为整数),则
(n为整数),则 的值等于______.(用含n的式子表示)
的值等于______.(用含n的式子表示)联系拓广:
如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,设
 ,则
,则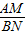 的值等于______.(用含m,n的式子表示)
的值等于______.(用含m,n的式子表示)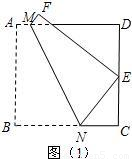

【答案】分析:如图(1-1),连接BM,EM,BE.由题设,得四边形ABNM和四边形FENM关于直线MN对称.由轴对称的性质知MN垂直平分BE.有BM=EM,BN=EN.由于四边形ABCD是正方形,则有∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.由 得,CE=DE=1;设BN=x,则NE=x,NC=2-x.在Rt△CNE中,由勾股定理知NE2=CN2+CE2.即x2=(2-x)2+12可解得x的值,从而得以BN的值,在Rt△ABM和在Rt△DEM中,由勾股定理知AM2+AB2=BM2,DM2+DE2=EM2,有AM2+AB2=DM2+DE2.
得,CE=DE=1;设BN=x,则NE=x,NC=2-x.在Rt△CNE中,由勾股定理知NE2=CN2+CE2.即x2=(2-x)2+12可解得x的值,从而得以BN的值,在Rt△ABM和在Rt△DEM中,由勾股定理知AM2+AB2=BM2,DM2+DE2=EM2,有AM2+AB2=DM2+DE2.
设AM=y,则DM=2-y,y2+22=(2-y)2+12可求得y的值,得到AM的值从而得到 .
.
解答: 解:(1)方法一:如图(1-1),连接BM,EM,BE.
解:(1)方法一:如图(1-1),连接BM,EM,BE.
由题设,得四边形ABNM和四边形FENM关于直线MN对称.
∴MN垂直平分BE,
∴BM=EM,BN=EN.
∵四边形ABCD是正方形,
∴∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.
∵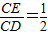 ,
,
∴CE=DE=1.
设BN=x,则NE=x,NC=2-x.
在Rt△CNE中,NE2=CN2+CE2.
∴x2=(2-x)2+12,
解得x= ,即BN=
,即BN= .
.
在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,
∴AM2+AB2=DM2+DE2.
设AM=y,则DM=2-y,
∴y2+22=(2-y)2+12,
解得y= ,即AM=
,即AM= (6分)
(6分)
∴ .
.
方法二:同方法一,BN= .
.
如图(1-2),过点N做NG∥CD,交AD于点G,连接BE.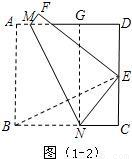
∵AD∥BC,
∴四边形GDCN是平行四边形.
∴NG=CD=BC.
同理,四边形ABNG也是平行四边形.
∴AG=BN=
∵MN⊥BE,∴∠EBC+∠BNM=90度.
∵NG⊥BC,∴∠MNG+∠BNM=90°,
∴∠EBC=∠MNG.
在△BCE与△NGM中
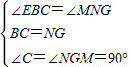 ,
,
∴△BCE≌△NGM,EC=MG.
∵AM=AG-MG,AM= -1=
-1= .
.
∴ .
.
(2)如图1,当四边形ABCD为正方形时,连接BE, =
= ,
,
不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n-x)2+12,x= ;
;
作MH⊥BC于H,则MH=BC,
又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,
∴NH=EC=1,AM=BH=BN-NH=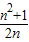 -1=
-1=
则: =
=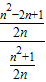 =
= .
.
故当 =
= ,则
,则 的值等于
的值等于 ;若
;若 =
= ,则
,则 的值等于
的值等于 ;
;
(3)若四边形ABCD为矩形,连接BE, =
=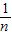 ,不妨令CD=n,则CE=1;
,不妨令CD=n,则CE=1;
又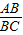 =
= =
= ,则BC=mn,同样的方法可求得:
,则BC=mn,同样的方法可求得:
BN= ,
,
BE⊥MN,易证得:△MHN∽△BCE.故 =
= ,
,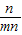 =
= ,
,
HN= ,故AM=BH=BN-HN=
,故AM=BH=BN-HN= ,
,
故 =
=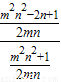 =
= .
.
故答案为: ;
;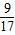 ;
;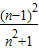 ;
; .
.
点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、正方形和矩形的性质,勾股定理求解.
 得,CE=DE=1;设BN=x,则NE=x,NC=2-x.在Rt△CNE中,由勾股定理知NE2=CN2+CE2.即x2=(2-x)2+12可解得x的值,从而得以BN的值,在Rt△ABM和在Rt△DEM中,由勾股定理知AM2+AB2=BM2,DM2+DE2=EM2,有AM2+AB2=DM2+DE2.
得,CE=DE=1;设BN=x,则NE=x,NC=2-x.在Rt△CNE中,由勾股定理知NE2=CN2+CE2.即x2=(2-x)2+12可解得x的值,从而得以BN的值,在Rt△ABM和在Rt△DEM中,由勾股定理知AM2+AB2=BM2,DM2+DE2=EM2,有AM2+AB2=DM2+DE2.设AM=y,则DM=2-y,y2+22=(2-y)2+12可求得y的值,得到AM的值从而得到
 .
.解答:
 解:(1)方法一:如图(1-1),连接BM,EM,BE.
解:(1)方法一:如图(1-1),连接BM,EM,BE.由题设,得四边形ABNM和四边形FENM关于直线MN对称.
∴MN垂直平分BE,
∴BM=EM,BN=EN.
∵四边形ABCD是正方形,
∴∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.
∵
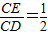 ,
,∴CE=DE=1.
设BN=x,则NE=x,NC=2-x.
在Rt△CNE中,NE2=CN2+CE2.
∴x2=(2-x)2+12,
解得x=
 ,即BN=
,即BN= .
.在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,
∴AM2+AB2=DM2+DE2.
设AM=y,则DM=2-y,
∴y2+22=(2-y)2+12,
解得y=
 ,即AM=
,即AM= (6分)
(6分)∴
 .
.方法二:同方法一,BN=
 .
.如图(1-2),过点N做NG∥CD,交AD于点G,连接BE.

∵AD∥BC,
∴四边形GDCN是平行四边形.
∴NG=CD=BC.
同理,四边形ABNG也是平行四边形.
∴AG=BN=

∵MN⊥BE,∴∠EBC+∠BNM=90度.
∵NG⊥BC,∴∠MNG+∠BNM=90°,
∴∠EBC=∠MNG.
在△BCE与△NGM中
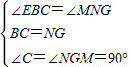 ,
,∴△BCE≌△NGM,EC=MG.
∵AM=AG-MG,AM=
 -1=
-1= .
.∴
 .
.(2)如图1,当四边形ABCD为正方形时,连接BE,
 =
= ,
,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n-x)2+12,x=
 ;
;作MH⊥BC于H,则MH=BC,
又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,
∴NH=EC=1,AM=BH=BN-NH=
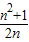 -1=
-1=
则:
 =
=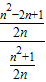 =
= .
.故当
 =
= ,则
,则 的值等于
的值等于 ;若
;若 =
= ,则
,则 的值等于
的值等于 ;
;(3)若四边形ABCD为矩形,连接BE,
 =
=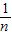 ,不妨令CD=n,则CE=1;
,不妨令CD=n,则CE=1; 又
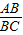 =
= =
= ,则BC=mn,同样的方法可求得:
,则BC=mn,同样的方法可求得:BN=
 ,
,BE⊥MN,易证得:△MHN∽△BCE.故
 =
= ,
,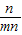 =
=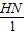 ,
,HN=
 ,故AM=BH=BN-HN=
,故AM=BH=BN-HN= ,
,故
 =
=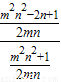 =
= .
.
故答案为:
 ;
;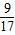 ;
;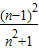 ;
; .
.点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、正方形和矩形的性质,勾股定理求解.

练习册系列答案
相关题目