题目内容
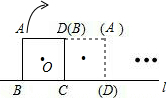
如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是1cm2,则它移动的距离AA′等于 cm.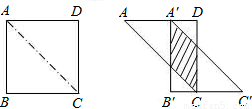
【答案】分析:本题考查了等腰直角三角形的判定和性质及平移的基本性质.
解答: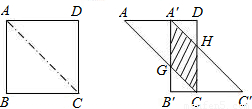 解:设CD与A′C′交于点H,AC与A′B′交于点G,
解:设CD与A′C′交于点H,AC与A′B′交于点G,
由平移的性质知,A′B′与CD平行且相等,∠ACB′=45°,∠DHA′=∠DA′H=45°,
∴△DA′H是等腰直角三角形,A′D=DH,四边形A′GCH是平行四边形,
∵SA′GCH=HC•B′C=(CD-DH)•DH=1,
∴DH=A′D=1,
∴AA′=AD-A′D=1.
故答案为1.
点评:本题需要运用等腰直角三角形的判定和性质及平移的基本性质结合求解.注意平移不改变图形的形状和大小;经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
解答:
 解:设CD与A′C′交于点H,AC与A′B′交于点G,
解:设CD与A′C′交于点H,AC与A′B′交于点G,由平移的性质知,A′B′与CD平行且相等,∠ACB′=45°,∠DHA′=∠DA′H=45°,
∴△DA′H是等腰直角三角形,A′D=DH,四边形A′GCH是平行四边形,
∵SA′GCH=HC•B′C=(CD-DH)•DH=1,
∴DH=A′D=1,
∴AA′=AD-A′D=1.
故答案为1.
点评:本题需要运用等腰直角三角形的判定和性质及平移的基本性质结合求解.注意平移不改变图形的形状和大小;经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
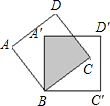 如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
| A、30° | B、35° |
| C、45° | D、60° |
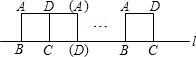 如图,将边长为2cm的正方形的四边沿直线l向右滚动(不滑动),当正方形滚动一周时,正方形的顶点A所经过的路线的长是
如图,将边长为2cm的正方形的四边沿直线l向右滚动(不滑动),当正方形滚动一周时,正方形的顶点A所经过的路线的长是
 (2012•遵义)如图,将边长为
(2012•遵义)如图,将边长为 如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为