题目内容
把一根长为100cm的铁丝截成n小段(n≥3),每段长不小于10cm,若对不论怎样的截法,总存在3小段.以它们为边可拼成一个三角形,则n的最小值是
- A.4
- B.5
- C.6
- D.7
D
分析:不防设其中最小的两段都是10cm,根据三角形的三边关系,即三角形的两边之和大于第三边,则若要至少拼成一个三角形的话,最小的两边的和要比第三边长,从而确定n的取值范围,即可求解.
解答:由题意知3≤n≤10,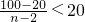 ,
,
则n>6,
即n的最小值是7.
故选D.
点评:此题考查了三角形的三边关系,能够根据三角形的三边关系解决生活中的实际问题.
分析:不防设其中最小的两段都是10cm,根据三角形的三边关系,即三角形的两边之和大于第三边,则若要至少拼成一个三角形的话,最小的两边的和要比第三边长,从而确定n的取值范围,即可求解.
解答:由题意知3≤n≤10,
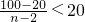 ,
,则n>6,
即n的最小值是7.
故选D.
点评:此题考查了三角形的三边关系,能够根据三角形的三边关系解决生活中的实际问题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目