题目内容
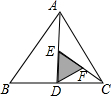在三角形ABC中，点D，E，F分别为BC，AD，CE的中点，且S△ABC=16，则S△DEF=
- A.2
- B.8
- C.4
- D.1
A
分析：利用等底同高的三角形面积相等，可求S△DEF．
解答：∵D是BC的中点，
∴S△ADC=
S△ABC=8，
又∵E，F分别为AD，EC的中点，
∴S△DCE=S△ADC=4，
S△DEF=S△ACE=2．
故选A．
点评：此题考查了中线的性质，主要根据等底等高来求各个小三角形的面积是大三角形的面积的一半．
分析：利用等底同高的三角形面积相等，可求S△DEF．
解答：∵D是BC的中点，
∴S△ADC=
S△ABC=8，又∵E，F分别为AD，EC的中点，
∴S△DCE=
S△ADC=4，S△DEF=
S△ACE=2．故选A．
点评：此题考查了中线的性质，主要根据等底等高来求各个小三角形的面积是大三角形的面积的一半．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
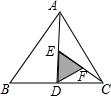在三角形ABC中，点D，E，F分别为BC，AD，CE的中点，且S△ABC=16，则S△DEF=（ ）| A、2 | B、8 | C、4 | D、1 |
在三角形ABC中，点O是AC边上一个动点，过点O作MN∥BC，设MN交∠BCA的平分线于点E，交△ABC的外角∠ACD平分线于点E．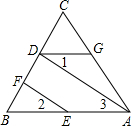
如图，在三角形ABC中，点D、F在边BC上，点E在边AB上，点G在边AC上，AD∥EF，∠1+∠FEA=180°．
