题目内容
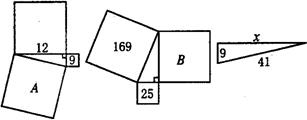
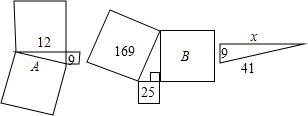根据下图中的数据，确定A=15
15
，B=144
144
，x=40
40
．分析：图1是已知两条直角边，可直接利用勾股定理求出A；
图2已知以斜边为边的正方形的面积和以一条直角边为边正方形的面积，根据勾股定理易求B；
图3已知一斜边和一直角边，可利用勾股定理求出另一直角边．
图2已知以斜边为边的正方形的面积和以一条直角边为边正方形的面积，根据勾股定理易求B；
图3已知一斜边和一直角边，可利用勾股定理求出另一直角边．
解答：解：图1观察可知，已知两条直角边分别是12、9，
则A2=122+92=225，
解得A=15；
图2观察可知，已知以斜边为边的正方形的面积和以一条直角边为边正方形的面积，
则B=169-25=144；
图3观察可知，已知一斜边等于41，一直角边等于9，
则x2=412-92=1600，
解得x=40．
故答案是15；144；40．
则A2=122+92=225，
解得A=15；
图2观察可知，已知以斜边为边的正方形的面积和以一条直角边为边正方形的面积，
则B=169-25=144；
图3观察可知，已知一斜边等于41，一直角边等于9，
则x2=412-92=1600，
解得x=40．
故答案是15；144；40．
点评：本题考查了勾股定理，解题的关键是根据图能分清直角边和斜边，并能使用勾股定理求边的长．
练习册系列答案
名校课堂系列答案
相关题目
下表给出了代数式x2+bx+c与x的一些对应值：
（1）根据表格中的数据，确定b、c的值，并填齐表格空白处的对应值；
（2）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
（2）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
下表给出了代数式x2+bx+c与x的一些对应值：
（1）根据表格中的数据，确定b、c的值，并填齐表格中空白处的对应值；
（2）代数式x2+bx+c是否有最小值？如果有，求出最小值；如果没有，请说明理由；
（3）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P点为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| X2+bx+c | … | 3 | -1 | 3 | … |
（2）代数式x2+bx+c是否有最小值？如果有，求出最小值；如果没有，请说明理由；
（3）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P点为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
