题目内容
【题目】如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿长方形BCDE的边作环绕运动．物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2017次相遇地点的坐标是 ．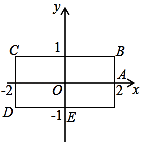 
【答案】（﹣1，1）
【解析】解：矩形的边长为4和2，因为物体乙是物体甲的速度的2倍，时间相同，物体甲与物体乙的路程比为1：2，由题意知： 第一次相遇物体甲与物体乙行的路程和为12×1，物体甲行的路程为12× 
=4，物体乙行的路程为12× 
=8，在BC边相遇；
第二次相遇物体甲与物体乙行的路程和为12×2，物体甲行的路程为12×2× =8，物体乙行的路程为12×2× =16，在DE边相遇；
第三次相遇物体甲与物体乙行的路程和为12×3，物体甲行的路程为12×3× =12，物体乙行的路程为12×3× =24，在A点相遇；
…
此时甲乙回到原出发点，则每相遇三次，两点回到出发点，
∵2015÷3=671…2，
故两个物体运动后的第2015次相遇地点的是：第二次相遇地点，
即物体甲行的路程为12×2× =8，物体乙行的路程为12×2× =16，在DE边相遇；
此时相遇点的坐标为：（﹣1，1）．
故答案为：（﹣1，1）．
利用行程问题中的相遇问题，由于矩形的边长为4和2，物体乙是物体甲的速度的2倍，求得每一次相遇的地点，找出规律即可解答．
练习册系列答案
相关题目
