题目内容
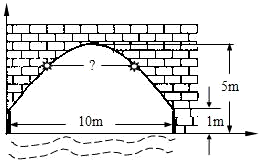 如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是
如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是
- A.3m
- B.4m
- C.5m
- D.6m
C
分析:根据抛物线在坐标系的位置,可知抛物线的顶点坐标为(5,5),抛物线的左端点坐标为(0,1),可设抛物线的顶点式求解析式,再根据两灯的纵坐标值,求横坐标,作差即可.
解答:抛物线的顶点坐标为(5,5),且经过点(0,1),
设抛物线解析式为y=a(x-5)2+5,
把点(0,1)代入得:
1=a(0-5)2+5,即a=-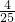 ,
,
∴抛物线解析式为y=-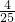 (x-5)2+5.
(x-5)2+5.
令y=4,得x1=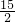 ,x2=
,x2= ,
,
∴盏景观灯之间的水平距离是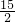 -
- =5m.
=5m.
故选C.
点评:根据抛物线在坐标系中的位置及点的坐标特点,合理地设抛物线解析式,再运用解析式解答题目的问题.
分析:根据抛物线在坐标系的位置,可知抛物线的顶点坐标为(5,5),抛物线的左端点坐标为(0,1),可设抛物线的顶点式求解析式,再根据两灯的纵坐标值,求横坐标,作差即可.
解答:抛物线的顶点坐标为(5,5),且经过点(0,1),
设抛物线解析式为y=a(x-5)2+5,
把点(0,1)代入得:
1=a(0-5)2+5,即a=-
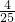 ,
,∴抛物线解析式为y=-
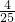 (x-5)2+5.
(x-5)2+5.令y=4,得x1=
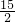 ,x2=
,x2= ,
,∴盏景观灯之间的水平距离是
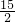 -
- =5m.
=5m.故选C.
点评:根据抛物线在坐标系中的位置及点的坐标特点,合理地设抛物线解析式,再运用解析式解答题目的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
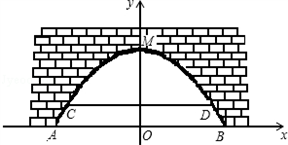
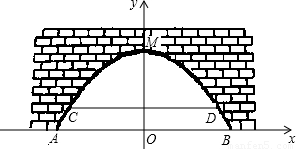
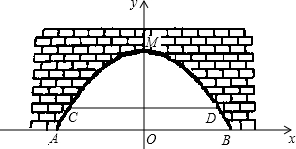 如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.
如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.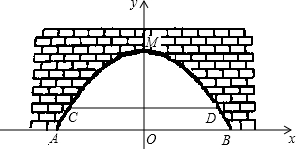 如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.
如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.