��Ŀ����
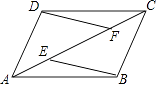
����Ŀ����������ABCD����ͼ1�������»�����
��1�λ������ֱ�����������ABCD�Աߵ��е�����ͼ2�������߶�HF��EG�����ǽ��ڵ�M����ʱͼ2�й���5����������
��2�λ�������ͼ2���Ͻ�������AEMH������������ͼ3����ͼ3�й���9����������
��1����ÿ�ζ������Ͻǵ�������һ�λ�����ȥ�����100�λ��ֺ���ͼ�й���______����������
��2������������ȥ���ڼ��λ��ֺ�����805����������д�����������
��3���ܷ���������ABCD���ֳ���2018�������ε�ͼ�����������������ǵڼ��λ����������������˵��������
��4�������ԭ�����εı߳�Ϊ1��ͨ�����ϵطָ�����Ϊ1��������������������ϵ�ͼ���ͼ������ؽ�����������Ժ����õ�һЩ������������̽������������ʽ�Ľ������
����![]() .��ֱ��д���𰸼�����
.��ֱ��д���𰸼�����
���𰸡���1��401����2��201����3�����ܣ���4��![]() ��
��
�������������������1���۲�ͼ�οɵõ�һ�οɵ�5�������Σ��ڶ��οɵ�9�������Σ������οɵ�13�������Σ��ɴ˿ɵõ�n�οɵ���4n+1���������Σ���n=100�������⣻��2����4n+1=805���ⷽ�̼�����⣻��3����4n+1=2018���ⷽ�̼����жϣ���4������ɿ������漸����������⣬������ô𰸣�
���������
��1���ߵ�һ�οɵ�5�������Σ��ڶ��οɵ�9�������Σ������οɵ�13�������Σ����n�οɵ���4n+1���������Σ����100�οɵ������Σ�4��100+1=401��������
�ʴ�Ϊ��401��
��2����������ã�4n+1=805����ã�n=201��
���201�λ��ֺ�����805�������Σ�
��3�����ܣ���4n+1=2018����ã�n=504.25����n������������ܽ���������ABCD���ֳ���2018�������ε�ͼ�Σ�
��4��![]()
=![]()

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�����Ŀ��Ϊ�˽�ס��������˶�Ա������ѵ������������ǽ����˸��ٲ��ԣ���������ʮ�ܵIJ��Գɼ����Ƴ���ͼ��ʾ������ͳ��ͼ��������涨���������ܲ��Գɼ�70�����ϣ�����70�֣�Ϊ���ʣ� 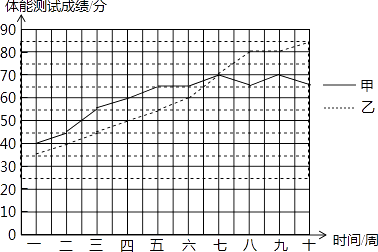
��1�������ͼ�����ṩ����Ϣ��д�±���
ƽ���� | ��λ�� | ���ܲ��Գɼ��ϸ������ | |
�� | 65 | ||
�� | 60 |
��2���������������ͬ�ĽǶȶ��˶�Ա���ܲ��Խ�������жϣ� ������ƽ������ɼ��ϸ�Ĵ����Ƚϼ��ң�˭�����ܲ��Գɼ��Ϻã�
������ƽ��������λ���Ƚϼ��ң�˭�����ܲ��Գɼ��Ϻã�
��3����������ͳ��ͼ�ͳɼ��ϸ�Ĵ�����������λ�˶�Ա����ѵ����Ч���Ϻã�