题目内容
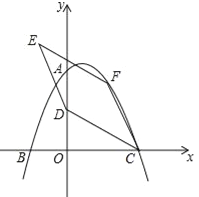
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
【答案】(1)![]() ,C(8,0);(2)①50;②18.
,C(8,0);(2)①50;②18.
【解析】
试题分析:(1)把A点和B点坐标代入![]() 得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
(2)①连结OF,如图,设F(t,![]() ),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=
),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=![]() ,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,![]() ),然后把E(t﹣8,
),然后把E(t﹣8,![]() )代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
试题解析:(1)把A(0,8),B(﹣4,0)代入![]() ,得:
,得:![]() ,解得:
,解得:![]() ,所以抛物线的解析式为
,所以抛物线的解析式为![]() ;
;
当y=0时,![]() ,解得
,解得![]() ,
,![]() ,所以C点坐标为(8,0);
,所以C点坐标为(8,0);
(2)①连结OF,如图,设F(t,![]() ),∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,∴S△CDF=S△ODF+S△OCF﹣S△OCD=
),∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,∴S△CDF=S△ODF+S△OCF﹣S△OCD=![]() =
=![]() =
=![]() ;
;
当t=3时,△CDF的面积有最大值,最大值为25,∵四边形CDEF为平行四边形,∴S的最大值为50;
②∵四边形CDEF为平行四边形,∴CD∥EF,CD=EF,∵点C向左平移8个单位,再向上平移4个单位得到点D,∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,![]() ),∵E(t﹣8,
),∵E(t﹣8,![]() )在抛物线上,∴
)在抛物线上,∴ ![]() ,解得t=7,当t=7时,S△CDF=
,解得t=7,当t=7时,S△CDF=![]() =9,∴此时S=2S△CDF=18.
=9,∴此时S=2S△CDF=18.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】为了解全市九年级学生某次数学模拟考试情况,现从全市30000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
分数段 | 频数 | 频率 |
x<60 | 20 | 0.10 |
60≤x<70 | 28 | 0.14 |
70≤x<80 | 54 | 0.27 |
80≤x<90 | a | 0.20 |
90≤x<100 | 24 | 0.12 |
100≤x<110 | 18 | b |
110≤x<120 | 16 | 0.08 |
请根据以上图表提供的信息,解答下列问题:
(1)表格中的a= ,b= ;
(2)请补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市30000名九年级学生中本次数学模拟考试成绩为优秀的学生约有多少名?