题目内容
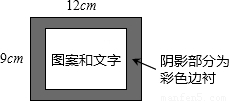
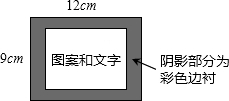 如图所示是一幅连环画的布局设计,整个页面是一个长12cm,宽9cm的大矩形,中间的图案和文字部分是一个与大矩形相似的小矩形.如果要使四周的彩色边衬所占面积是大矩形面积的
如图所示是一幅连环画的布局设计,整个页面是一个长12cm,宽9cm的大矩形,中间的图案和文字部分是一个与大矩形相似的小矩形.如果要使四周的彩色边衬所占面积是大矩形面积的 ,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
解:因为小矩形与大矩形相似,所以小矩形的长与宽之比为4:3,
设小矩形的长为4xcm,小矩形的宽为3xcm.
根据题意,得4x•3x= ×12×9.
×12×9.
解得x1=2 ,x2=-2
,x2=-2 (不合题意,舍去).
(不合题意,舍去).
所以上、下边衬的均为( -3
-3 )cm,左、右边衬的宽均为(6-4
)cm,左、右边衬的宽均为(6-4 )cm.
)cm.
分析:因为小矩形与大矩形相似,所以小矩形的长与宽之比为4:3,设小矩形的长为4xcm,小矩形的宽为3xcm,根据如果要使四周的彩色边衬所占面积是大矩形面积可列方程求解.
点评:本题考查理解题意的能力,关键是看出小矩形长和宽的关系,然后以面积做为等量关系列方程求解.
设小矩形的长为4xcm,小矩形的宽为3xcm.
根据题意,得4x•3x=
 ×12×9.
×12×9.解得x1=2
 ,x2=-2
,x2=-2 (不合题意,舍去).
(不合题意,舍去).所以上、下边衬的均为(
 -3
-3 )cm,左、右边衬的宽均为(6-4
)cm,左、右边衬的宽均为(6-4 )cm.
)cm.分析:因为小矩形与大矩形相似,所以小矩形的长与宽之比为4:3,设小矩形的长为4xcm,小矩形的宽为3xcm,根据如果要使四周的彩色边衬所占面积是大矩形面积可列方程求解.
点评:本题考查理解题意的能力,关键是看出小矩形长和宽的关系,然后以面积做为等量关系列方程求解.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
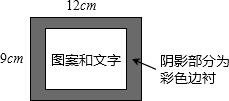 如图所示是一幅连环画的布局设计,整个页面是一个长12cm,宽9cm的大矩形,中间的图案和文字部分是一个与大矩形相似的小矩形.如果要使四周的彩色边衬所占面积是大矩形面积的
如图所示是一幅连环画的布局设计,整个页面是一个长12cm,宽9cm的大矩形,中间的图案和文字部分是一个与大矩形相似的小矩形.如果要使四周的彩色边衬所占面积是大矩形面积的 ,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?