Question

如图，某港口有一灯塔A，灯塔A的正东有B、C两灯塔，以BC为直径的半圆区域内有若干暗礁，BC=18海里，一船在M处测得灯塔A、C分别在船的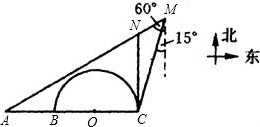南偏西60°和南偏西15°方向，船沿MA方向行驶6海里恰好处在灯塔C的正北方向N处．
（1）求CN的长（精确到0.1海里）；
（2）若船继续沿MA方向朝A行驶，是否有触礁的危险？
（参考数值：

2

=1.414，

3

=1.732，sin15°=0.2588，cos15°=0.9658，tan15°=0.2680，cot15°=3.732）

Answer 1

分析：（1）设BC的中点是O，作ND⊥CM，OE⊥AM．求CN的长，可以在直角△NCD中利用三角函数求解．
（2）判断是否有触礁危险可以计算出OE的长，然后比较与9海里的大小关系就可以．

解答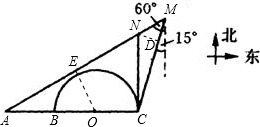：解：（1）设BC的中点为O，作ND⊥CM，OE⊥AM，垂足分别为D、E．
在直角△MND中，ND=MN•sin∠NMD=6•sin45°=3

2

（海里），
在直角△NCD中，CN=

ND

sin15°

≈16.4海里．

（2）在直角△ANC中，AC=CN•cotA=16.4•cot30°=16.4×

3

≈28.4海里，
∴AO=AC-

1

2

BC=28.4-

1

2

×18≈19.4（海里），
∴OE=

1

2

AO≈

1

2

×19.4=9.7（海里），
∵9.7＞9，
所以船继续沿MA方向朝A行驶，没有触礁的危险．

点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．