题目内容
【题目】若∠AOB=45°,P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1 , P2 , 连接OP1 , OP2 , 则下列结论正确的是( )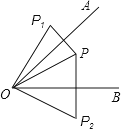
A.OP1⊥OP2
B.OP1=OP2
C.OP1≠OP2
D.OP1⊥OP2且OP1=OP2
【答案】D
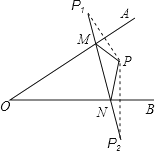
【解析】如图,∵点P关于直线OA、OB的对称点P1、P2 ,
∴OP1=OP2=OP ,
∠AOP=∠AOP1 , ∠BOP=∠BOP2 ,
∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2 ,
=2(∠AOP+∠BOP),
=2∠AOB ,
∵∠AOB=45°,
∴OP1⊥OP2成立.
故选D.
【考点精析】利用轴对称的性质对题目进行判断即可得到答案,需要熟知关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】某种油菜籽在相同条件下发芽试验的结果如下:
每批粒数 | 100 | 400 | 800 | 1000 | 2000 | 4000 |
发芽的频数 | 85 | 300 | 652 | 793 | 1604 | 3204 |
发芽的频率 | 0.850 | 0.750 | 0.815 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计该油菜种子发芽的概率为_______(精确到0.1).