题目内容
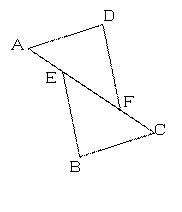
如图，在△AFD和△CEB中，点A、E、F、C在同一条直线上，有下列四个论断：①AD=CB ②AD∥BC ③AE=CF ④∠D=∠B
用其中的三个作为条件，不能得到△ADF≌△CBE的三个条件的序号
- A.①②③
- B.①②④
- C.②③④
- D.①③④
D
分析：把四个论断取3个进行组合，看是否能够得到△ADF≌△CBE，做题时根据已知条件，结合全等的判定方法逐一验证．
解答：（1）根据全等三角形的判定（ASA）可得
AD=CB，AD∥BC?∠A=∠C，∠D=∠B．故△ADF≌△CBE
可选①②④；
（2）根据全等三角形的判定（SAS）可得
AD=CB，AD∥BC?∠A=∠C，AE=CF?AF=CE，故△ADF≌△CBE
可选①②③；
（3）根据全等三角形的判定（SAS）可得
AD∥BC?∠A=∠C，AE=CF?AF=CE，∠D=∠B，故△ADF≌△CBE
可选②③④．
故选D．
点评：本题考查的是全等三角形的判定定理．一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
分析：把四个论断取3个进行组合，看是否能够得到△ADF≌△CBE，做题时根据已知条件，结合全等的判定方法逐一验证．
解答：（1）根据全等三角形的判定（ASA）可得
AD=CB，AD∥BC?∠A=∠C，∠D=∠B．故△ADF≌△CBE
可选①②④；
（2）根据全等三角形的判定（SAS）可得
AD=CB，AD∥BC?∠A=∠C，AE=CF?AF=CE，故△ADF≌△CBE
可选①②③；
（3）根据全等三角形的判定（SAS）可得
AD∥BC?∠A=∠C，AE=CF?AF=CE，∠D=∠B，故△ADF≌△CBE
可选②③④．
故选D．
点评：本题考查的是全等三角形的判定定理．一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
练习册系列答案
相关题目
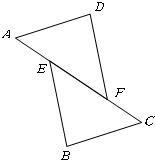31、如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，有下面四个论断：①AD=CB，②AE=CF，③∠B=∠D，④AD∥BC．请用其中三个作为已知条件，余下一个作为求证结论，编一道数学问题，并写出解答过程：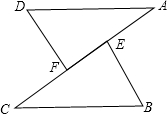
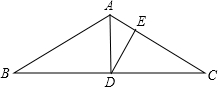
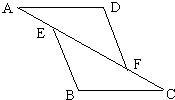18、如图，在△AFD和△CEB中，点A、E、F、C在同一条直线上，有下列四个论断：①AD=CB ②AD∥BC ③AE=CF ④∠D=∠B
如图，在△AFD和△CEB中，点A，E，F，C在同一直线上，已知AE=CF，∠B=∠D，AD∥BC．