题目内容
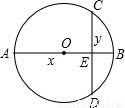
善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于E),设AE=x,BE=y,他用含x,y的式子表示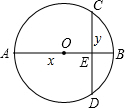 图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式
图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式分析:此题中隐含的不等关系:直径是圆中最长的弦,所以AB≥CD.
首先可以表示出AB=x+y,再根据相交弦定理的推论和垂径定理,得CD=2CE=2
.
首先可以表示出AB=x+y,再根据相交弦定理的推论和垂径定理,得CD=2CE=2
| xy |
解答:解:根据相交弦定理的推论,得CE2=AE•BE,则CE=
.
根据垂径定理,得CE2=AE•BE,
即(
CD)2=xy,
∴CD=2CE=2
.
又AB=x+y,且AB≥CD,得x+y≥2
.
| xy |
根据垂径定理,得CE2=AE•BE,
即(
| 1 |
| 2 |
∴CD=2CE=2
| xy |
又AB=x+y,且AB≥CD,得x+y≥2
| xy |
点评:本题考查:直径是圆中最长的弦;相交弦定理的推论以及垂径定理的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 弦
弦 于
于 ),设
),设 ,
, ,他用含
,他用含 的式子表示图中的弦
的式子表示图中的弦 的大小关系,发现了一个关于正数
的大小关系,发现了一个关于正数
 弦
弦 于
于 ),设
),设 ,
, ,他用含
,他用含 的式子表示图中的弦
的式子表示图中的弦 的大小关系,发现了一个关于正数
的大小关系,发现了一个关于正数