��Ŀ����
��ͼ��A��B���������ֱ��ǣ�8��0������0��6������P�ɵ�B������BA�������A������ֱ���˶����ٶ�Ϊÿ��3����λ���ȣ���Q��A������AO��OΪ����ԭ�㣩�������O������ֱ���˶����ٶ�Ϊÿ��2����λ���ȣ�����PQ�������˶�ʱ��Ϊt��0��t��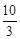 ���룮����������⣺
���룮����������⣺
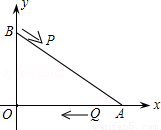
��1����tΪ��ֵʱ��PQ��BO��
��2�����AQP�����ΪS��
����S��t֮��ĺ�����ϵʽ�������S�����ֵ��
�������ǹ涨����P��Q������ֱ�Ϊ��x1��y1������x2��y2�����������꣨x2��x1��y2��y1����Ϊ������PQ�������꣮��Sȡ���ֵʱ��������PQ�������꣮
��1����t=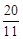 ��ʱ��PQ��BO��2����S=
��ʱ��PQ��BO��2����S=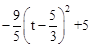 ��0��t��
��0��t�� ����5�ڣ�
����5�ڣ�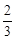 ����3��
����3��
���������⣺��1����A��B���������ֱ��ǣ�8��0������0��6������OB=6��OA=8��
��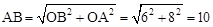 ��
��

��ͼ�٣���PQ��BOʱ��AQ=2t��BP=3t����AP=10��3t��
��PQ��BO���� ����
����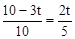 �����t=
�����t=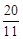 ��
��
�൱t=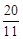 ��ʱ��PQ��BO��
��ʱ��PQ��BO��
��2���ɣ�1��֪��OA=8��OB=6��AB=10��
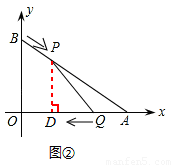
����ͼ����ʾ������P��PD��x���ڵ�D��
��PD��BO��
���APD�ס�ABO��
��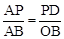 ����
����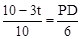 �����PD=6��
�����PD=6��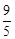 t��
t��
��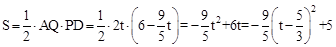 ��
��
��S��t֮��ĺ�����ϵʽΪ��S=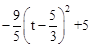 ��0��t��
��0��t�� ����
����
�൱t=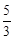 ��ʱ��Sȡ�����ֵ�����ֵΪ5��ƽ����λ����
��ʱ��Sȡ�����ֵ�����ֵΪ5��ƽ����λ����
����ͼ����ʾ����Sȡ���ֵʱ��t=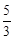 ��
��
��PD=6��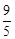 t=3����PD=
t=3����PD=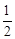 BO��
BO��
��PD��BO�����ʱPDΪ��OAB����λ�ߣ���OD=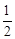 OA=4����P��4��3����
OA=4����P��4��3����
��AQ=2t= ����OQ=OA��AQ=
����OQ=OA��AQ=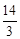 ����Q��
����Q��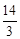 ��0����
��0����
�����⣬������PQ��������Ϊ��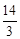 ��4��0��3��������
��4��0��3��������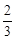 ����3����
����3����
�൱Sȡ���ֵʱ��������PQ��������Ϊ��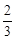 ����3����
����3����
��1����ͼ����ʾ����PQ��BOʱ������ƽ���߷��߶γɱ������������߶α���ʽ �����t��ֵ��
�����t��ֵ��
��2������S��ϵʽ��Ҫ������á�AQP�ĸߣ���ͼ����ʾ������P������P��PD��x���ڵ�D������ƽ����PD��BO���ɡ�APD�ס�ABO�� 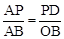 ���PD���Ӷ�S�������S��t֮��ĺ�����ϵʽ��һ������t�Ķ��κ��������ö��κ�����ֵ�ķ������S�����ֵ��
���PD���Ӷ�S�������S��t֮��ĺ�����ϵʽ��һ������t�Ķ��κ��������ö��κ�����ֵ�ķ������S�����ֵ��
�������P��Q�����꣺��Sȡ���ֵʱ�����Ƴ���ʱPDΪ��OAB����λ�ߣ��Ӷ��������P���ݺ����꣬������Q�����꣬�Ӷ���õ�P��Q�����ꣻ���P��Q������֮���롰����PQ������Ķ��壨x2��x1��y2��y1����������⡣

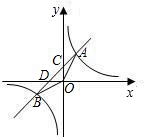 ��ͼ��һ�κ���y=kx+b��ͼ����һ�����������ޣ����뷴��������ͼ���ཻ��A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D��OB=
��ͼ��һ�κ���y=kx+b��ͼ����һ�����������ޣ����뷴��������ͼ���ཻ��A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D��OB= 8����ͼ���ӳ���A������B�����ֲ�ͬ�Ľ�ͨ���ߣ����������ɻ�����ȥ�ٶ����أ����ɻ���ʱ���������Ϊ
8����ͼ���ӳ���A������B�����ֲ�ͬ�Ľ�ͨ���ߣ����������ɻ�����ȥ�ٶ����أ����ɻ���ʱ���������Ϊ 20������ȥ����Ӱ��ʱ��������������Ļ��һЩ�������ֲ���Ϊ�˿���Ļ��Ե�ľ�ͷ��ͣ��ת���۾�����ͼ��ʾ����A��B�ֱ�Ϊ��Ļ��Ե���㣬������P�㣬���ӽ�Ϊ��APB���������õ�ӰԺ��P���ǹۿ������λ�ã������Ѿ������������ˣ���ô����ҵ�һ��λ��Q��ʹ����Q��P��������ͬ���ӽ�������ͼ�л�������������ͼ�ۼ�����д��������
20������ȥ����Ӱ��ʱ��������������Ļ��һЩ�������ֲ���Ϊ�˿���Ļ��Ե�ľ�ͷ��ͣ��ת���۾�����ͼ��ʾ����A��B�ֱ�Ϊ��Ļ��Ե���㣬������P�㣬���ӽ�Ϊ��APB���������õ�ӰԺ��P���ǹۿ������λ�ã������Ѿ������������ˣ���ô����ҵ�һ��λ��Q��ʹ����Q��P��������ͬ���ӽ�������ͼ�л�������������ͼ�ۼ�����д�������� ��2013•�ӱ�һģ����ͼ����ֱ֪��y=x+4������???��ֱ���A��B���㣬��C��Բ������Ϊ ��2��O�����뾶Ϊ2����D�ǡ�C�ϵ�һ�����㣬�߶�DA��y�ύ�ڵ�E�����ABE�������Сֵ�����ֵ�ֱ���
��2013•�ӱ�һģ����ͼ����ֱ֪��y=x+4������???��ֱ���A��B���㣬��C��Բ������Ϊ ��2��O�����뾶Ϊ2����D�ǡ�C�ϵ�һ�����㣬�߶�DA��y�ύ�ڵ�E�����ABE�������Сֵ�����ֵ�ֱ���