题目内容
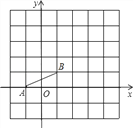
【题目】如图,已知以点A(0,1)、C(1,0)为顶点的△ABC中,∠BAC=60°,∠ACB=90°,在坐标系内有一动点P(不与A重合),以P、B、C为顶点的三角形和△ABC全等,则P点坐标为____________.
【答案】(2,-1)、![]() 、
、![]()
【解析】解:由勾股定理得:AC=![]() ,∵∠BAC=60°,∠ACB=90°,∴AB=
,∵∠BAC=60°,∠ACB=90°,∴AB=![]() ,BC=
,BC=![]() ,分为三种情况:
,分为三种情况:
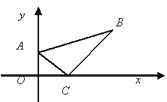
①如图1,延长AC到P,使AC=CP,连接BP,过P作PM⊥x轴于M,此时PM=OA=1,CM=OC=1,OM=1+1=2,即P的坐标是(2,﹣1);
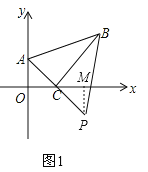
②如图2,过B作BP⊥BC,且BP=AC=![]() ,此时PC=AB=
,此时PC=AB=![]() .过P作PM⊥x轴于M,此时∠PCM=15°,在x轴上取一点N,使∠PNM=30°,即CN=PN,设PM=x,则CN=PN=2x,MN=
.过P作PM⊥x轴于M,此时∠PCM=15°,在x轴上取一点N,使∠PNM=30°,即CN=PN,设PM=x,则CN=PN=2x,MN=![]() x,在Rt△CPM中,由勾股定理得:(
x,在Rt△CPM中,由勾股定理得:(![]() )2=(2x+
)2=(2x+![]() x)2+x2,x=
x)2+x2,x=![]() ,即PM=
,即PM=![]() ,MC=2x+
,MC=2x+![]() x=
x=![]() ,OM=1+
,OM=1+![]() =
=![]() ,即P的坐标是(
,即P的坐标是(![]() ,
, ![]() );
);

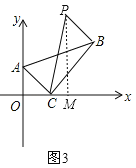
③如图3,过B作BP⊥BC,且BP=AC=![]() ,过P作PM⊥x轴于M,此时∠PCM=30°+45°=75°,∠CPM=15°,和③解法类似求出CM=
,过P作PM⊥x轴于M,此时∠PCM=30°+45°=75°,∠CPM=15°,和③解法类似求出CM=![]() ,PM=2x+
,PM=2x+![]() x=
x=![]() ,OM=1+
,OM=1+![]() =
=![]() ,即P的坐标是(
,即P的坐标是(![]() ,
, ![]() ).
).
故答案为:(2,﹣1)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目