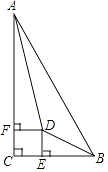Question

【题目】以线段AC为对角线的凸四边形ABCD（它的四个顶点A、B、C、D按顺时针方向排列，每个内角均小于180°），已知AB=BC=CD，∠ABC=120°，∠CAD=30°，则∠BCD的大小为____________．

Answer 1

【答案】60°或120°

【解析】

∵AB=BC, ∠ABC=120°，

∴∠1=∠2=∠CAD=30°，

∴AD∥BC，

如图1，过点C分别作CE⊥AB于E，CF⊥AD于F，

∵∠1=∠CAD，

∴CE=CF，

在Rt△ACE与Rt△ACF中，

∵AC=AC，

CE=CF，

∴Rt△ACE≌Rt△ACF，

∴∠ACE=∠ACF，

在Rt△BCE与Rt△DCF中，

∵CB=CD，

CE=CF，

∴Rt△BCE≌Rt△DCF，

∴∠BCE=∠DCF，

∴∠2=∠ACD=30°，

∴∠BCD=60°；

如图2,

∵AD∥BC,AB=CD′，

∴四边形ABCD′是等腰梯形，

∴∠BCD′=∠ABC=120°.

所以∠BCD=60°或120°.