题目内容
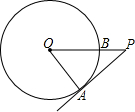 已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据切线的性质,△OAP是直角三角形,根据勾股定理就可以求出OP=5,则可以求得cos∠APO的值.
解答:解:∵PA为⊙O的切线,A为切点,
∴OA⊥AP.
又PA=4,OA=3,∴OP=5.
∴cos∠APO=
.
故本题选D.
∴OA⊥AP.
又PA=4,OA=3,∴OP=5.
∴cos∠APO=
| 4 |
| 5 |
故本题选D.
点评:本题运用了切线的性质定理,通过切线的性质定理得到△OAP是直角三角形,是解决本题的关键.

练习册系列答案
相关题目
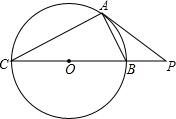 已知:如图,PA为⊙O的切线,A为切点,割线PBC过圆心O,PA=4,PB=2.
已知:如图,PA为⊙O的切线,A为切点,割线PBC过圆心O,PA=4,PB=2. 已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )



 已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )







