题目内容
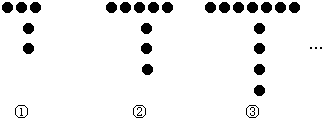
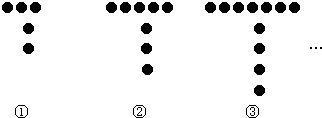
上面是用棋子摆成的“T”字,摆成第一个“T”字需要5枚棋子,摆成第二个“T”字需要8枚棋子,按这样的规律摆下去,若用2009枚棋子可以摆到第n个“T”,则n=
- A.667
- B.668
- C.669
- D.610
C
分析:根据图形中每个图案中棋子的个数,8-5=3、11-8=3、14-11=3可得出规律:每一个图形中棋子的个数比上一个图形中棋子的个数多3,所以第n个图案中,棋子的个数为5+3(n-1).由此求出n.
解答:由题意可得:
摆成第1个“T”字需要5个棋子;
摆成第2个“T”字需要8个棋子,8-5=3;
摆成第3个“T”字需要11个棋子,11-8=3;
摆成第4个“T”字需要14个棋子,14-11=3;
…,
由此可得出规律:摆成第n个“T”字需要5+3(n-1)=3n+2个棋子,
用2009枚棋子可以摆到第n个“T”,则:
3n+2=2009,
所以n=669.
故选:C.
点评:本题主要考查的是根据图中图形的变化情况,通过归纳与总结得出规律的能力,本题的关键在于相邻图形间棋子的变化个数.
分析:根据图形中每个图案中棋子的个数,8-5=3、11-8=3、14-11=3可得出规律:每一个图形中棋子的个数比上一个图形中棋子的个数多3,所以第n个图案中,棋子的个数为5+3(n-1).由此求出n.
解答:由题意可得:
摆成第1个“T”字需要5个棋子;
摆成第2个“T”字需要8个棋子,8-5=3;
摆成第3个“T”字需要11个棋子,11-8=3;
摆成第4个“T”字需要14个棋子,14-11=3;
…,
由此可得出规律:摆成第n个“T”字需要5+3(n-1)=3n+2个棋子,
用2009枚棋子可以摆到第n个“T”,则:
3n+2=2009,
所以n=669.
故选:C.
点评:本题主要考查的是根据图中图形的变化情况,通过归纳与总结得出规律的能力,本题的关键在于相邻图形间棋子的变化个数.

练习册系列答案
相关题目