题目内容
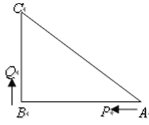
【题目】如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.

(1)求∠ACE的度数.
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
【答案】(1)∠ACE=45°;(2)详见解析.
【解析】
(1)先根据内角和定理求得∠ACB=90°,再由角平分线性质可得答案;
(2)根据CD⊥AB知∠BCD=90°-∠B=30°,∠FCD=∠ECB-∠BCD=15°,结合∠CDF=75°可得∠CFD=180°-∠FCD-∠CDF=90°,即可得证.
解:(1)∵∠A=30°,∠B=60°,
∴∠ACB=180°-∠A-∠B=90°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=![]() ∠ACB=45°;
∠ACB=45°;
(2)∵CD⊥AB,
∴∠CDB=90°,
∴∠BCD=90°-∠B=30°,
∴∠FCD=∠ECB-∠BCD=15°,
∵∠CDF=75°,
∴∠CFD=180°-∠FCD-∠CDF=90°,
∴△CFD是直角三角形.

练习册系列答案
相关题目