题目内容
课题:探究能拼成正多边形的三角形的面积计算公式.
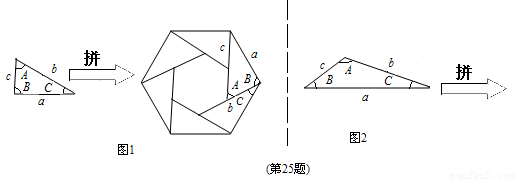
【小题1】如图1,三角形的三边长分别为a、b、c，∠A＝60°，现将六个这样的三角形（设面积为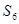
）拼成一个六边形，由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形，其面积可计算出为 ；由于所围成的小六边形的边长都是 ，其面积为 ，由此可得＝ .
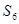【小题2】如图2, 三角形的三边长分别为a、b、c，∠A＝120°，试用这样的三角形拼成一个正三角形(设面积为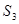
),先画出这个正三角形,再推出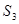的计算公式;
【小题3】推广:
对于三角形的三边长分别为a、b、c，当∠A取什么值时,能拼成一个任意正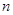
边形吗?如果能,试写出∠A和三角形的面积
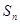的表达式;如果不能,请简要说明理由.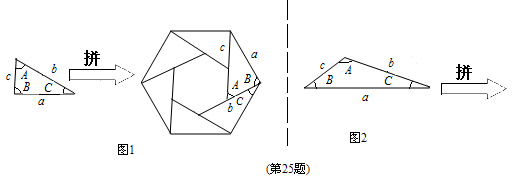
【小题1】解：（1）
, b－c ,
, 
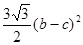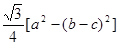
【小题2】如图2画出正三角形花环,
∵大三角形的边长都是a,小三角形的边长都是b－c,
∴两个三角形都是正三角形,
可求得大三角形面积为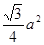
,小三角形的面积为
,∴=
=
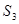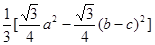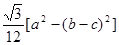
【小题3】当∠A=
时, 能拼成一个任意正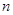边形花环,此时大正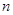边形的面积为
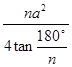,花环内小正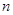边形的面积为
,∴=
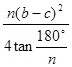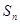解析
练习册系列答案
相关题目
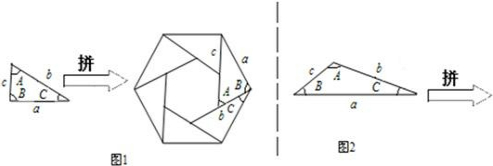
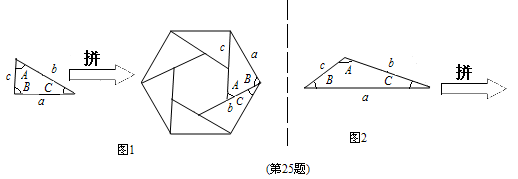
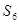）拼成一个六边形，由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形，其面积可计算出为 ；由于所围成的小六边形的边长都是 ，其面积为 ，由此可得
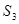),先画出这个正三角形,再推出
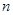边形吗?如果能,试写出∠A和三角形的面积
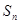的表达式;如果不能,请简要说明理由.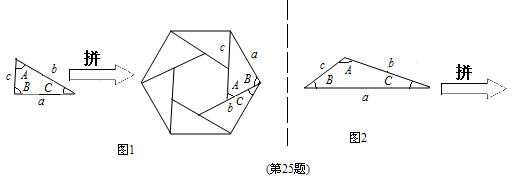
）拼成一个六边形，由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形，其面积可计算出为 ；由于所围成的小六边形的边长都是 ，其面积为 ，由此可得
),先画出这个正三角形,再推出
边形吗?如果能,试写出∠A和三角形的面积
的表达式;如果不能,请简要说明理由.
）拼成一个六边形，由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形，其面积可计算出为 ；由于所围成的小六边形的边长都是 ，其面积为 ，由此可得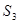
),先画出这个正三角形,再推出
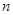边形吗?如果能,试写出∠A和三角形的面积
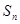的表达式;如果不能,请简要说明理由.