��Ŀ����
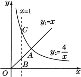
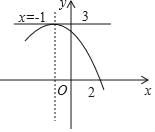
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ���㣨2��0������Գ�����ֱ��x=��1��ֱ��y=3ǡ�þ������㣮�������жϣ��ٵ�x����2ʱ��y��x�������С�� ��ac��0�� ��a��b+c��0�� �ܷ���ax2+bx+c=0����������x1=2��x2=��4���ݵ�m��3ʱ������ax2+bx+c=m��ʵ������������ȷ���ǣ�������
A. �٢ڢ� B. �٢ڢ� C. �ڢܢ� D. �ڢۢ�
���𰸡�C
��������
�������ߵĿ��ڷ����ж�a��0�Ĺ�ϵ������������y��Ľ����ж�c��0�Ĺ�ϵ��Ȼ����ݶԳ��ἰ��������x�ύ������������������������ý��۽����жϣ�
����ͼ��֪����x��-2ʱ��y��x��������ʴ���
�������߿��ڷ������£���a��0��
��������y�ύ�������ᣬ��c��0��
����ac��0������ȷ��
��������֪����x=-1ʱ��y=3��0��
����a-b+c��0���ʴ���
��������֪����������x�����һ������㣨2��0������ֱ��x=-1�Գƣ������������x�����һ���������ǣ�-4��0�������Է���ax2+bx+c=0����������x1=2��x2=-4������ȷ��
��������֪����m��3ʱ��ֱ��y=m��������y=ax2+bx+c��a��0���н��㣬���ԣ�����ax2+bx+c=m��ʵ����������ȷ��
������������ȷ�Ľ����ǣ��ڢܢ���
��ѡ��C��

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�