题目内容
如下图,在等腰△ABC中,AB=AC,∠BAC=120 °,AD为BC边上的高,过点D作DE∥AB,交AC于点E,图中除△ABC外,还有等腰三角形吗?若有,请指出,并说明理由。

解:△ADE是等边三角形;△DEC为等腰三角形。
理由:因为AB=AC,∠BAC=120°,
所以∠B=∠C=30°,
因为DE∥AB,
所以∠EDC=∠B=30°,
所以△DEC为等腰三角形,
因为AD⊥BC,
所以∠DAE= ∠BAC=
∠BAC=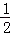 ×120°=60°,
×120°=60°,
因为∠ADC=90°,所以∠ADE=60°,
所以△ADE是等边三角形。
理由:因为AB=AC,∠BAC=120°,
所以∠B=∠C=30°,
因为DE∥AB,
所以∠EDC=∠B=30°,
所以△DEC为等腰三角形,
因为AD⊥BC,
所以∠DAE=
 ∠BAC=
∠BAC=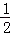 ×120°=60°,
×120°=60°,因为∠ADC=90°,所以∠ADE=60°,
所以△ADE是等边三角形。

练习册系列答案
相关题目
 27、如下图,在等腰梯形ABCD中,AD∥BC,AB∥DE,∠C=60°,AD=7,AB=9,求梯形的周长?
27、如下图,在等腰梯形ABCD中,AD∥BC,AB∥DE,∠C=60°,AD=7,AB=9,求梯形的周长?
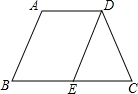 如下图,在等腰梯形ABCD中,AD∥BC,AB∥DE,∠C=60°,AD=7,AB=9,求梯形的周长?
如下图,在等腰梯形ABCD中,AD∥BC,AB∥DE,∠C=60°,AD=7,AB=9,求梯形的周长?