题目内容
在直角坐标系x0y中,一次函数y=
x+
的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD=∠ABD,求图象经过B、D两点的一次函数的解析式.
| ||
| 3 |
| 2 |
分析:点D在x轴上,且∠BCD=∠ABD,则D的位置可以在C的左侧,也可以在C的右侧,即D的横坐标x大于1和小于1两种情况.
当x>1时,易证△BCD∽△ABD,CD、BD都可以利用x表示出来,根据相似三角形的对应边的比相等,即可得到关于x的方程,求得x的值,即可得到D的坐标,然后利用待定系数法即可求得直线的解析式;
当x<1时,可证△ABC∽△ADB,与上面的方法相同,可以求得直线的解析式.
当x>1时,易证△BCD∽△ABD,CD、BD都可以利用x表示出来,根据相似三角形的对应边的比相等,即可得到关于x的方程,求得x的值,即可得到D的坐标,然后利用待定系数法即可求得直线的解析式;
当x<1时,可证△ABC∽△ADB,与上面的方法相同,可以求得直线的解析式.
解答: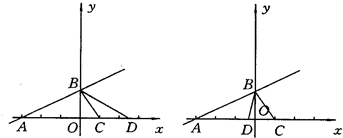 解:∵点A、B分别是直线y=
解:∵点A、B分别是直线y=
x+
与x轴和y轴交点,
∴A(-3,0),B(0,
),
∵点C坐标(1,0)由勾股定理得BC=
,AB=
,
设点D的坐标为(x,0).
(1)当点D在C点右侧,即x>1时,
∵∠BCD=∠ABD,∠BDC=∠ADB,
∴△BCD∽△ABD,
∴
=
,
∴
=
①
∴
=
,∴8x2-22x+5=0,
∴x1=
,x2=
,经检验:x1=
,x2=
,都是方程①的根,
∵x=
,不合题意,∴舍去,∴x=
,∴D点坐标为(
,0).
设图象过B、D两点的一次函数解析式为y=kx+b,
∴
∴所求一次函数为y=-
x+
;
(2)若点D在点C左侧则x<1,可证△ABC∽△ADB,
∴
=
,∴
=
②
∴8x2-18x-5=0,
∴x1=-
,x2=
,经检验x1=-
,x2=
,都是方程②的根.
∵x2=
不合题意舍去,
∴x1=-
,
∴D点坐标为(-
,0),
∴图象过B、D(-
,0)两点的一次函数解析式为y=4
x+
,
综上所述,满足题意的一次函数为y=-
x+
或y=4
x+
.
 解:∵点A、B分别是直线y=
解:∵点A、B分别是直线y=
| ||
| 3 |
| 2 |
∴A(-3,0),B(0,
| 2 |
∵点C坐标(1,0)由勾股定理得BC=
| 3 |
| 11 |
设点D的坐标为(x,0).
(1)当点D在C点右侧,即x>1时,
∵∠BCD=∠ABD,∠BDC=∠ADB,
∴△BCD∽△ABD,
∴
| BC |
| AB |
| CD |
| BD |
∴
| ||
|
| |x-1| | ||
|
∴
| 3 |
| 11 |
| x2-2x+1 |
| x2+2 |
∴x1=
| 5 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |
| 1 |
| 4 |
∵x=
| 1 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
设图象过B、D两点的一次函数解析式为y=kx+b,
|
|
∴所求一次函数为y=-
2
| ||
| 5 |
| 2 |
(2)若点D在点C左侧则x<1,可证△ABC∽△ADB,
∴
| AD |
| AB |
| BD |
| CB |
| |x+3| | ||
|
| ||
|
∴8x2-18x-5=0,
∴x1=-
| 1 |
| 4 |
| 5 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |
∵x2=
| 5 |
| 2 |
∴x1=-
| 1 |
| 4 |
∴D点坐标为(-
| 1 |
| 4 |
∴图象过B、D(-
| 1 |
| 4 |
| 2 |
| 2 |
综上所述,满足题意的一次函数为y=-
2
| ||
| 5 |
| 2 |
| 2 |
| 2 |
点评:本题考查了相似三角形的判定与性质,待定系数法求函数的解析式,正确求得D的坐标是关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
在直角坐标系x0y中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )个
| A.1个 | B.2个 | C.3个 | D.4个 |
