题目内容
如图，等腰△ABC一腰AC上的高BD与底边BC的夹角为37°，则顶角为 °．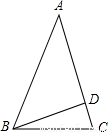
【答案】分析：根据高的定义求出∠BDC，根据三角形的内角和定理求出∠C，根据等腰三角形的性质求出∠ABC，根据三角形的内角和定理求出即可．
解答：解：∵BD是△ABC的高，
∴∠BDC=90°，
∵∠DBC=37°，
∴∠C=53°，
∵AB=AC，
∴∠C=∠ABC=53°，
∴∠A=180°-∠ABC-∠C=180°-53°-53°=74°．
故答案为：74．
点评：本题主要考查对等腰三角形的性质，三角形的高的定义，三角形的内角和定理等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．
解答：解：∵BD是△ABC的高，
∴∠BDC=90°，
∵∠DBC=37°，
∴∠C=53°，
∵AB=AC，
∴∠C=∠ABC=53°，
∴∠A=180°-∠ABC-∠C=180°-53°-53°=74°．
故答案为：74．
点评：本题主要考查对等腰三角形的性质，三角形的高的定义，三角形的内角和定理等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．
练习册系列答案
相关题目
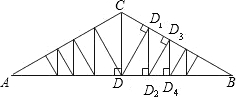如图，等腰△ABC中，AC=BC，CD是底边上的高，∠A=30°．（1）CD与AB有什么数量关系？请说明理由；
（2）过点D作DD1⊥BC，垂足为D1；D1D2⊥AB，垂足为D2；D2D3⊥BC，垂足为D3；D3D4⊥AB，垂足为D4；…；D2n+1D2n⊥AB，垂足为D2n；D2n+1D2n⊥BC，垂足为D2n+1（n为非零自然数）．若CD=a，请用含a的代数式表示下表中线段的长度（请将结果直接填入表中）；
| 线段 |
D1D2 | D3D4 | D5D6 | … | D2n-1 D2n | ||
| 长度 |
|
… |
2、如图，等腰△ABC一腰AC上的高BD与底边BC的夹角为37°，则顶角为
如图，等腰△ABC中，一腰AB的垂直平分线交AC于E，已知AB=12cm，△BCE周长为20cm，那么底边BC=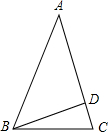
如图，等腰△ABC一腰AC上的高BD与底边BC的夹角为37°，则顶角为________°．