题目内容
(2004•嘉兴)如图,Rt△OAB的斜边OA在x轴的正半轴上,直角的顶点B在第一象限内,已知点A(10,0),△OAB的面积为20.(1)求B点的坐标;
(2)求过O、B、A三点抛物线的解析式;
(3)判断该抛物线的顶点P与△OAB的外接圆的位置关系,并说明理由.

【答案】分析:(1)过B作BC⊥OA于C,根据三角形OAB的面积可求出BC=4,然后可设OC=x,根据射影定理可得出BC2=OC•AC,据此可求出x的值,即可得出B点坐标;
(2)已知了三点的坐标,可用待定系数法求出抛物线的解析式;
(3)根据抛物线和圆的对称性可知,P和三角形OAB的外心必在抛物线的对称轴上,因此本题只需判断P点的纵坐标的绝对值与OA的一半的大小关系,如果|yP|大于5,则顶点P在圆外,如果|yP|小于5,则在园内,如果等于5,则在圆上.
解答: 解:(1)过B作BC⊥OA于C,
解:(1)过B作BC⊥OA于C,
∵S△OAB= OA•BC=20,OA=10,
OA•BC=20,OA=10,
∴BC=4
在直角三角形ABO中,BC⊥OA,
设OC=x,根据射影定理有:
BC2=OC•AC,即16=x(10-x),解得x=2,x=8
因此B(2,4);
(2)设抛物线的解析式为y=ax(x-10),
已知抛物线过B(2,4),有:
a×2×(2-10)=4,a=-
∴所求的抛物线解析式为:y=- x2+
x2+ x;
x;
(3)由(2)可知:y=- (x-5)2+
(x-5)2+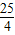
因此P(5, )
)
∵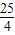 >5
>5
∴顶点P在外接圆外.
点评:本题主要考查了二次函数、圆、直角三角形的相关知识.
(2)已知了三点的坐标,可用待定系数法求出抛物线的解析式;
(3)根据抛物线和圆的对称性可知,P和三角形OAB的外心必在抛物线的对称轴上,因此本题只需判断P点的纵坐标的绝对值与OA的一半的大小关系,如果|yP|大于5,则顶点P在圆外,如果|yP|小于5,则在园内,如果等于5,则在圆上.
解答:
 解:(1)过B作BC⊥OA于C,
解:(1)过B作BC⊥OA于C,∵S△OAB=
 OA•BC=20,OA=10,
OA•BC=20,OA=10,∴BC=4
在直角三角形ABO中,BC⊥OA,
设OC=x,根据射影定理有:
BC2=OC•AC,即16=x(10-x),解得x=2,x=8
因此B(2,4);
(2)设抛物线的解析式为y=ax(x-10),
已知抛物线过B(2,4),有:
a×2×(2-10)=4,a=-

∴所求的抛物线解析式为:y=-
 x2+
x2+ x;
x;(3)由(2)可知:y=-
 (x-5)2+
(x-5)2+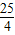
因此P(5,
 )
)∵
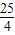 >5
>5∴顶点P在外接圆外.
点评:本题主要考查了二次函数、圆、直角三角形的相关知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



