题目内容
(2013•怀柔区二模)下列函数中,其图象与x轴有两个交点的是( )
分析:通过二次函数的图象的开口方向,顶点坐标即可判断其图象与x轴的交点个数.
解答:解:A、∵y=
(x-23)2+2013的图象的顶点在第一象限,开口向上,
∴与x轴无交点.
故本选项错误;
B、∵y=
(x+23)2+2013的图象顶点在第二象限,开口向上,
∴与x轴无交点;
故本选项错误;
C、∵y=-
(x-23)2-2013的图象顶点在第四象限,开口向下,
∴与x轴无交点;
故本选项错误;
D、∵y=-
(x+23)2+2013的图象的顶点在第二象限,开口向下,
∴与x轴有两个交点.
故选D.
| 2 |
| 5 |
∴与x轴无交点.
故本选项错误;
B、∵y=
| 2 |
| 5 |
∴与x轴无交点;
故本选项错误;
C、∵y=-
| 2 |
| 5 |
∴与x轴无交点;
故本选项错误;
D、∵y=-
| 2 |
| 5 |
∴与x轴有两个交点.
故选D.
点评:本题考查了抛物线与x轴的交点问题,是基础知识要熟练掌握.

练习册系列答案
相关题目
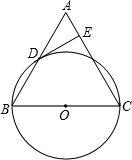 (2013•怀柔区二模)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(2013•怀柔区二模)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.