题目内容
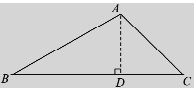
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
【答案】(1)(10![]() +10)m;(2)超速.
+10)m;(2)超速.
【解析】
试题分析:(1)利用∠B=30°,∠C=45°,AD=10,求出BD=10![]() ,DC=10,从而得出BC=10
,DC=10,从而得出BC=10![]() +10
+10
(2)利用![]() ,
,![]() ,求出BC
,求出BC![]() 27,再求出v=108千米/小时>80千米/小时,故超速。
27,再求出v=108千米/小时>80千米/小时,故超速。
试题解析:(1)如图,过点A作AD⊥BC于点D,则AD=10m
∵在RtΔACD中,∠C=45°
∴RtΔACD是等腰直角三角形
∴CD=AD=10m
在RtΔABD中,tanB=![]()
∵∠B=30°
∴![]()
∴BD=10![]() m
m
∴BC=BD+DC=(10![]() +10)m
+10)m
(2)这辆汽车超速.理由如下.
由(1)知BC=(10![]() +10)m,又
+10)m,又![]()
∴BC=27m
∴汽车速度v=![]() =30(m/s)
=30(m/s)
又30 m/s=108km/h,此地限速为80 km/h
∵108>80
∴这辆汽车超速.

练习册系列答案
相关题目