题目内容
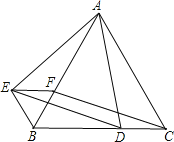
【题目】如图,凸四边形ABCD中,AB∥CD,且AB+BC=CD+AD.求证:ABCD是平行四边形。
【答案】详见解析.
证明:假设ABCD不是平行四边形,即AB≠CD,
不妨设AB>CD.在AB边上取点E,使AE=CD,则AECD是平行四边形,
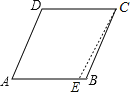
∴AD=CE,
由AB+BC=CD+AD,
即(AE+EB)+BC=CD+AD,
∴EB+BC=CE,与三角形不等式EB+BC>CE矛盾,
因此,ABCD必是平行四边形。
【解析】试题分析:
利用已知条件不能直接证明四边形ABCD是平行四边形,故考虑用反证法,假设四边形ABCD不是平行四边形,则可设AB>CD,所以在AB上取点E,使AE=CD,然后经过推理得出矛盾,从而假设不成立,故原命题成立.
试题解析:
证明:假设ABCD不是平行四边形,即AB≠CD,
不妨设AB>CD.在AB边上取点E,使AE=CD,则AECD是平行四边形,

∴AD=CE,
由AB+BC=CD+AD,
即(AE+EB)+BC=CD+AD,
∴EB+BC=CE,与三角形不等式EB+BC>CE矛盾,
因此,ABCD必是平行四边形。

练习册系列答案
相关题目
【题目】某公司欲聘请一位员工,三位应聘者A、B、C的原始评分如下表:
应聘者 | 仪表 | 工作经验 | 电脑操作 | 社交能力 | 工作效率 |
A | 4 | 5 | 5 | 3 | 3 |
B | 4 | 3 | 3 | 5 | 4 |
C | 3 | 3 | 4 | 4 | 4 |
(1)如果按五项原始评分的平均分,应聘用谁;
(2)如果按仪表、工作经验、电脑操作、社交能力、工作效率的原始评分分别占10%,15%,20%,25%,30%综合评分,谁将被聘用?为什么?