题目内容
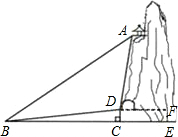 如图,某旅游区有一个景观奇异的望天洞,点D是洞的入口,游人从入口进洞游览后,要经山洞到达山顶的出口凉亭A处观赏旅游区风景,最后做缆车沿索道AB返回山脚下的B处.在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在A处测得的仰角∠ABC=40°,在D处测得的仰角∠ADF=45°,过点D做地面BE的垂线,垂足为点C.
如图,某旅游区有一个景观奇异的望天洞,点D是洞的入口,游人从入口进洞游览后,要经山洞到达山顶的出口凉亭A处观赏旅游区风景,最后做缆车沿索道AB返回山脚下的B处.在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在A处测得的仰角∠ABC=40°,在D处测得的仰角∠ADF=45°,过点D做地面BE的垂线,垂足为点C.(1)求∠ADB的度数;
(2)求索道AB的长(结果仅保留根号).
分析:(1)利用点D处的周角即可求得∠ADB的度数;
(2)首先分析图形,根据题意构造直角三角形.本题涉及到两个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
(2)首先分析图形,根据题意构造直角三角形.本题涉及到两个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
解答: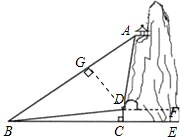 解:(1)∵DC⊥CE,
解:(1)∵DC⊥CE,
∴∠BCD=90°.
又∵∠DBC=10°,
∴∠BDC=80°,
∵∠ADF=85°,
∴∠ADB=360°-80°-90°-85°=105°.
(2)过点D作DG⊥AB于点G.
在Rt△GDB中,
∠GBD=40°-10°=30°,
∴∠BDG=90°-30°=60°.
又∵BD=100米,
∴GD=
BD=100×
=50米.
∴GB=BD×cos30°=100×
=50
米.
在Rt△ADG中,∠ADG=105°-60°=45°,
∴GD=GA=50米. (8分)
∴AB=AG+GB=(50+50
)米.
答:索道AB的长(50+50
)米.
 解:(1)∵DC⊥CE,
解:(1)∵DC⊥CE,∴∠BCD=90°.
又∵∠DBC=10°,
∴∠BDC=80°,
∵∠ADF=85°,
∴∠ADB=360°-80°-90°-85°=105°.
(2)过点D作DG⊥AB于点G.
在Rt△GDB中,
∠GBD=40°-10°=30°,
∴∠BDG=90°-30°=60°.
又∵BD=100米,
∴GD=
| 1 |
| 2 |
| 1 |
| 2 |
∴GB=BD×cos30°=100×
| ||
| 2 |
| 3 |
在Rt△ADG中,∠ADG=105°-60°=45°,
∴GD=GA=50米. (8分)
∴AB=AG+GB=(50+50
| 3 |
答:索道AB的长(50+50
| 3 |
点评:本题考查仰角的定义及直角三角形的解法.首先构造直角三角形,再借助角边关系、三角函数的定义解题是关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
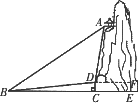
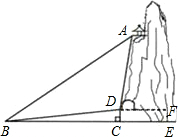 如图,某旅游区有一个景观奇异的望天洞,点D是洞的入口,游人从入口进洞游览后,要经山洞到达山顶的出口凉亭A处观赏旅游区风景,最后做缆车沿索道AB返回山脚下的B处.在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在A处测得的仰角∠ABC=40°,在D处测得的仰角∠ADF=45°,过点D做地面BE的垂线,垂足为点C.
如图,某旅游区有一个景观奇异的望天洞,点D是洞的入口,游人从入口进洞游览后,要经山洞到达山顶的出口凉亭A处观赏旅游区风景,最后做缆车沿索道AB返回山脚下的B处.在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在A处测得的仰角∠ABC=40°,在D处测得的仰角∠ADF=45°,过点D做地面BE的垂线,垂足为点C.