题目内容
（2000•台州）已知正多边形的边心距与边长的比为
，则此正多边形为（ ）A．正三角形
B．正方形
C．正六边形
D．正十二边形
【答案】分析：边心距与边长的比为
，即边心距等于边长的一半，进而可知半径与边心距的夹角是45度．可求出中心角的度数，从而得到正多边形的边数．
解答：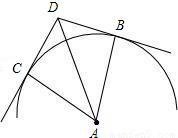
解：如图，圆A是正多边形的内切圆；
∠ACD=∠ABD=90°，AC=AB，CD=BD是边长的一半，
当正多边形的边心距与边长的比为
，即如图有AB=BD，
则△ABD是等腰直角三角形，
∠BAD=45°，∠CAB=90°，
即正多边形的中心角是90度，
所以它的边数=360÷90=4．
故选B．
点评：本题利用了正多边形与它的内切圆的关系求解，转化为解直角三角形的计算．
，即边心距等于边长的一半，进而可知半径与边心距的夹角是45度．可求出中心角的度数，从而得到正多边形的边数．解答：
解：如图，圆A是正多边形的内切圆；∠ACD=∠ABD=90°，AC=AB，CD=BD是边长的一半，
当正多边形的边心距与边长的比为
，即如图有AB=BD，则△ABD是等腰直角三角形，
∠BAD=45°，∠CAB=90°，
即正多边形的中心角是90度，
所以它的边数=360÷90=4．
故选B．
点评：本题利用了正多边形与它的内切圆的关系求解，转化为解直角三角形的计算．
练习册系列答案
相关题目
的图象分别交x轴，y轴于A，C两点．
的图象分别交x轴，y轴于A，C两点．