题目内容
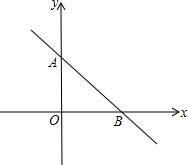已知如图直角坐标系上有两点A（0，2），B（
，0），在x轴上有一点P，且△PAB是等腰三角形，写出点P的坐标．
解：∵A（0，2），B（，0），
∴AB=4．
设P（x，0）．
①当AP=AB时，点P与点B关于y轴对称，则P1（-，0）；
②当BP=AB时，|x-2
|=4，
解得，x=4+2，或x=-4+2，
即P2（4+2，0）、P3（-4+2，0）；
③当PA=PB时，|x-2|=
，
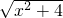解得，x=
，即P4（，0）．
综上所述，符合条件的点P的坐标分别为：P1（-，0）；P2（4+2，0）、P3（-4+2，0）、P4（，0）．
分析：分类讨论：若AP=AB；若BP=AB；若PA=PB，分别求得点P的坐标．
点评：本题考查了等腰三角形的判定、坐标与图形性质．解答该题时，采用了分类讨论的解题方法，以防漏解．
，0），∴AB=4．
设P（x，0）．
①当AP=AB时，点P与点B关于y轴对称，则P1（-
，0）；②当BP=AB时，|x-2
|=4，解得，x=4+2
，或x=-4+2，即P2（4+2
，0）、P3（-4+2，0）；③当PA=PB时，|x-2
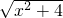|=，解得，x=
，即P4（，0）．综上所述，符合条件的点P的坐标分别为：P1（-
，0）；P2（4+2，0）、P3（-4+2，0）、P4（，0）．分析：分类讨论：若AP=AB；若BP=AB；若PA=PB，分别求得点P的坐标．
点评：本题考查了等腰三角形的判定、坐标与图形性质．解答该题时，采用了分类讨论的解题方法，以防漏解．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
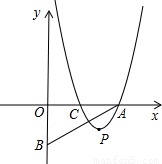
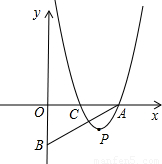
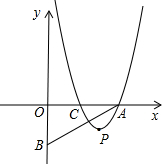已知，平面直角坐标系上有A（a，0）、B（0，-b）、C（b，0）三点，且a≥b＞0，抛物线y=（x-2）（x-m）-（n-2）（n-m）． （m，n为常数，且m+2≥2n＞0），经过点A和点C，顶点为P
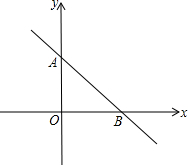已知如图直角坐标系上有两点A（0，2），B（
