题目内容
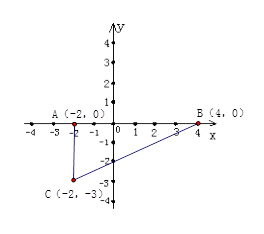
在平面直角坐标系中,点A的坐标是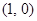 ,点B的坐标是
,点B的坐标是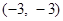 ,点C是y轴上一动点,要使△ABC为等腰三角形,则符合要求的点C的位置共有……………( )
,点C是y轴上一动点,要使△ABC为等腰三角形,则符合要求的点C的位置共有……………( )
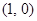 ,点B的坐标是
,点B的坐标是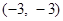 ,点C是y轴上一动点,要使△ABC为等腰三角形,则符合要求的点C的位置共有……………( )
,点C是y轴上一动点,要使△ABC为等腰三角形,则符合要求的点C的位置共有……………( )| A.2个 | B.3个 | C.4个 | D.5个 |
D
∵点A的坐标是(1,0),点B的坐标是(﹣3,﹣3),
∴AB=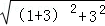 =5,
=5,
如图,①以点A为圆心AB的长为半径画弧,交y轴于C1和C2,
∴OC1=OC2=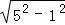 =2
=2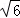 ,
,
∴可得C1(0,2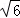 ),C2(0,﹣2
),C2(0,﹣2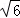 );
);
②以点B为圆心BA的长为半径画弧,交y轴于点C3和C4,
可得C3(0,1),C4(0,﹣7);
③AB的中垂线交y轴于点C5,
设直线AB的解析式为:y=kx+b,
∴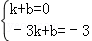 ,
,
解得: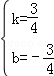 ,
,
∴直线AB的解析式为:y=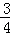 x﹣
x﹣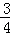 ,
,
∴OE=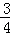 ,AE=
,AE=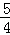 ,DE=
,DE=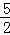 ﹣
﹣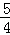 =
=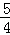 ,
,
∴△DEC5∽△OEA,
∴DE:OE=EC5:AE,
∴EC5=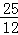 ,
,
∴OC5=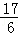 ,
,
∵C5(0,﹣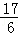 ).
).
∴符合要求的点C的为:C1(0,2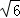 ),C2(0,﹣2
),C2(0,﹣2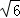 ),C3(0,1),C4(0,﹣7),C5(0,﹣
),C3(0,1),C4(0,﹣7),C5(0,﹣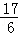 ).
).
故选D.
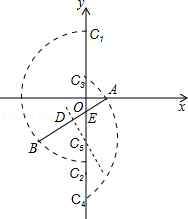
∴AB=
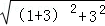 =5,
=5,如图,①以点A为圆心AB的长为半径画弧,交y轴于C1和C2,
∴OC1=OC2=
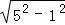 =2
=2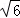 ,
,∴可得C1(0,2
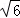 ),C2(0,﹣2
),C2(0,﹣2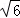 );
);②以点B为圆心BA的长为半径画弧,交y轴于点C3和C4,
可得C3(0,1),C4(0,﹣7);
③AB的中垂线交y轴于点C5,
设直线AB的解析式为:y=kx+b,
∴
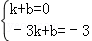 ,
,解得:
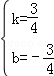 ,
,∴直线AB的解析式为:y=
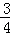 x﹣
x﹣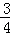 ,
,∴OE=
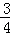 ,AE=
,AE=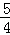 ,DE=
,DE=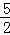 ﹣
﹣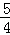 =
=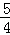 ,
,∴△DEC5∽△OEA,
∴DE:OE=EC5:AE,
∴EC5=
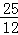 ,
,∴OC5=
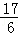 ,
,∵C5(0,﹣
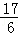 ).
).∴符合要求的点C的为:C1(0,2
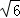 ),C2(0,﹣2
),C2(0,﹣2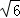 ),C3(0,1),C4(0,﹣7),C5(0,﹣
),C3(0,1),C4(0,﹣7),C5(0,﹣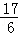 ).
).故选D.


练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目