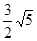题目内容
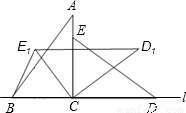
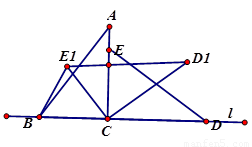
 如图,直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,将△ECD绕点C逆时针旋转到△E1CD1位置,且D1E1∥l,则B、E1两点之间的距离为________.
如图,直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,将△ECD绕点C逆时针旋转到△E1CD1位置,且D1E1∥l,则B、E1两点之间的距离为________.
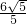
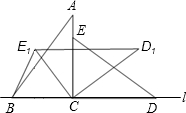
分析:根据题意作图构建直角三角形,然后根据旋转的性质得出对应边相等,利用直角三角形面积公式得出OC,在Rt△CE1F中,利用勾股定理得出CF,从而得出BF,在Rt△BFE1中,利用勾股定理即可得出BE1.
解答:
 解:过E1作E1F⊥BC,D1E1 与AC交于点O,如图:
解:过E1作E1F⊥BC,D1E1 与AC交于点O,如图:∵D1E1∥l,∠DCE=90°,
∴CO为△E1CD1的高,
在△E1CD1中,BC=CE=CE1=3,AC=CD=CD1=4,
根据勾股定理得:D1E1=5,
根据直角三角形面积公式
 CE1•CD1=
CE1•CD1= D1E1•CO,
D1E1•CO,解得:CO=
 =E1F,
=E1F,在Rt△CE1F中,利用勾股定理得:CF=
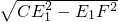 ,
,解得:CF=
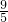 ,
,∴BF=BC-CF=3-
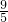 =
= ,
,在Rt△BFE1中,利用勾股定理得:BE1=
 ,
,解得:BE1=
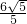 ,
,故答案为
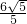 .
.点评:本题主要考查了旋转的性质、直角三角形面积公式、勾股定理等,综合性较强,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
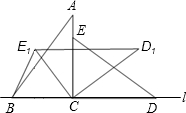 如图,直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,将△ECD绕点C逆时针旋转到△E1CD1位置,且D1E1∥l,则B、E1两点之间的距离为
如图,直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,将△ECD绕点C逆时针旋转到△E1CD1位置,且D1E1∥l,则B、E1两点之间的距离为
 C.
C.  D.
D. 
 C.
C.  D.
D.