题目内容
(2011湖南永州,22,8分)某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球、羽毛球拍和乒乓球拍,已知篮球、羽毛球拍和乒乓球拍的单价比为8︰3︰2,且其单价和为130元.
⑴请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?
⑵若要求购买篮球、羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是篮球数量的4倍,且购买乒乓球拍的数量不超过15副,请问有几种购买方案?
⑴请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?
⑵若要求购买篮球、羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是篮球数量的4倍,且购买乒乓球拍的数量不超过15副,请问有几种购买方案?
解:⑴因为篮球、羽毛球拍和乒乓球拍的单价比为8︰3︰2,所以,可以依次设它们的单价分别为 ,
,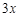 ,
,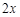 元,于是,得
元,于是,得 ,解得
,解得 .
.
所以,篮球、羽毛球拍和乒乓球拍的单价分别为80元、30元和20元.
⑵设购买篮球的数量为 个,则够买羽毛球拍的数量为
个,则够买羽毛球拍的数量为 副,购买乒乓球拍的数量为
副,购买乒乓球拍的数量为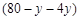 副,根据题意,得
副,根据题意,得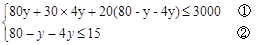
由不等式①,得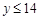 ,由不等式②,得
,由不等式②,得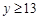 ,
,
于是,不等式组的解集为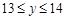 ,因为
,因为 取整数,所以
取整数,所以 只能取13或14.
只能取13或14.
因此,一共有两个方案:
方案一,当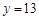 时,篮球购买13个,羽毛球拍购买52副,乒乓球拍购买15副;
时,篮球购买13个,羽毛球拍购买52副,乒乓球拍购买15副;
方案二,当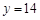 时,篮球购买14个,羽毛球拍购买56副,乒乓球拍购买10副.
时,篮球购买14个,羽毛球拍购买56副,乒乓球拍购买10副.
 ,
,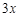 ,
,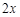 元,于是,得
元,于是,得 ,解得
,解得 .
.所以,篮球、羽毛球拍和乒乓球拍的单价分别为80元、30元和20元.
⑵设购买篮球的数量为
 个,则够买羽毛球拍的数量为
个,则够买羽毛球拍的数量为 副,购买乒乓球拍的数量为
副,购买乒乓球拍的数量为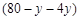 副,根据题意,得
副,根据题意,得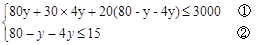
由不等式①,得
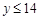 ,由不等式②,得
,由不等式②,得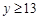 ,
,于是,不等式组的解集为
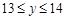 ,因为
,因为 取整数,所以
取整数,所以 只能取13或14.
只能取13或14.因此,一共有两个方案:
方案一,当
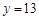 时,篮球购买13个,羽毛球拍购买52副,乒乓球拍购买15副;
时,篮球购买13个,羽毛球拍购买52副,乒乓球拍购买15副;方案二,当
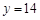 时,篮球购买14个,羽毛球拍购买56副,乒乓球拍购买10副.
时,篮球购买14个,羽毛球拍购买56副,乒乓球拍购买10副.略

练习册系列答案
相关题目
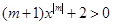 是关于
是关于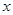 的一元一次不等式,则
的一元一次不等式,则 的取值是 .
的取值是 .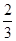 x-3k=5(x-k)+1的解是负数.
x-3k=5(x-k)+1的解是负数.  的值小于0,则可列不等式………………………………( )
的值小于0,则可列不等式………………………………( )
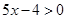
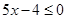

 元,以后每分钟收费
元,以后每分钟收费 元(不足1分钟按1分钟计).某天小芳给同学打了一个6分钟的市话,所用电话费为
元(不足1分钟按1分钟计).某天小芳给同学打了一个6分钟的市话,所用电话费为 元;小刚现准备给同学打市电话6分钟,他经过思考以后,决定先打3分钟,挂断后再打3分钟,这样只需电话费
元;小刚现准备给同学打市电话6分钟,他经过思考以后,决定先打3分钟,挂断后再打3分钟,这样只需电话费 元.如果你想给某同学打市话,准备通话10分钟,则你所需要的电话费至少为( )
元.如果你想给某同学打市话,准备通话10分钟,则你所需要的电话费至少为( ) 元
元 元
元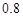 元
元 元
元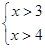 的解集的情况为( ).
的解集的情况为( ).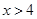
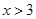

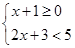
 的解集在数轴上表示为( ).
的解集在数轴上表示为( ).