题目内容
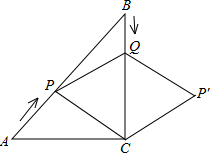 (2012•黄冈)如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒
(2012•黄冈)如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒| 2 |
分析:首先连接PP′交BC于O,根据菱形的性质可得PP′⊥CQ,可证出PO∥AC,根据平行线分线段成比例可得
=
,再表示出AP、AB、CO的长,代入比例式可以算出t的值.
| AP |
| AB |
| CO |
| CB |
解答: 解:连接PP′交BC于O,
解:连接PP′交BC于O,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴
=
,
∵设点Q运动的时间为t秒,
∴AP=
t,QB=t,
∴QC=6-t,
∴CO=3-
,
∵AC=CB=6,∠ACB=90°,
∴AB=6
,
∴
=
,
解得:t=2,
故选:B.
 解:连接PP′交BC于O,
解:连接PP′交BC于O,∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴
| AP |
| AB |
| CO |
| CB |
∵设点Q运动的时间为t秒,
∴AP=
| 2 |
∴QC=6-t,
∴CO=3-
| t |
| 2 |
∵AC=CB=6,∠ACB=90°,
∴AB=6
| 2 |
∴
| ||
6
|
3-
| ||
| 6 |
解得:t=2,
故选:B.
点评:此题主要考查了菱形的性质,勾股定理,平行线分线段成比例,关键是熟记平行线分线段成比例定理的推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.推出比例式
=
,再表示出所需要的线段长代入即可.
| AP |
| AB |
| CO |
| CB |

练习册系列答案
相关题目
 (2012•黄冈)如图,已知抛物线的方程C1:y=-
(2012•黄冈)如图,已知抛物线的方程C1:y=- (2012•黄冈)如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的直径为( )
(2012•黄冈)如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的直径为( )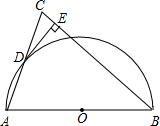 (2012•黄冈)如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(2012•黄冈)如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.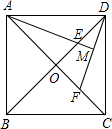 (2012•黄冈)如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
(2012•黄冈)如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.