题目内容
如图所示,平面直角坐标系中,Rt△ABC的直角边AC在x轴上,A(1,0),C(3,0),B(3,-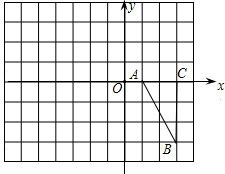 3).将先向左平移6个单位得到Rt△A1B1C1,再将Rt△A1B1C1绕A1点逆时针旋转90°得到Rt△A1B2C2.
3).将先向左平移6个单位得到Rt△A1B1C1,再将Rt△A1B1C1绕A1点逆时针旋转90°得到Rt△A1B2C2.(1)请在直角坐标系中画出Rt△A1B1C1和Rt△A1B2C2.
(2)请你结合图象变换的知识回答:Rt△A1B2C2能否直接由Rt△ABC绕某一点P逆时针旋转角α(0<α<360)而来?若能,请你直接写出P点的坐标及旋转角α的度数;若不能,请说明理由;
(3)在直接将Rt△ABC绕P点逆时针旋转角α得到Rt△A1B2C2的过程中,求线段BC在旋转过程中扫过图形的面积.
分析:(1)根据平移和旋转的性质找出A、B、C变换后的对应点,后顺次连接即可;
(2)根据图象位置变化性质,可以找出旋转中心,即旋转转角度;
(3)利用扇形面积求出即可.
(2)根据图象位置变化性质,可以找出旋转中心,即旋转转角度;
(3)利用扇形面积求出即可.
解答:解:(1)如图:
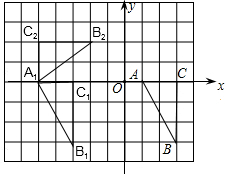
(2)P(-2,-3),逆时针旋转90度;
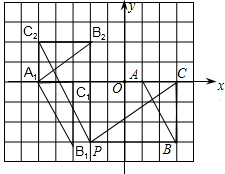
(3)BC在旋转过程中扫过图形的面积为:
S=
=
π.

(2)P(-2,-3),逆时针旋转90度;

(3)BC在旋转过程中扫过图形的面积为:
S=
| 90π(34-25) |
| 360 |
| 9 |
| 4 |
点评:此题主要考查了平移与旋转的性质与三角形,考查了学生的动手能力.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。