题目内容
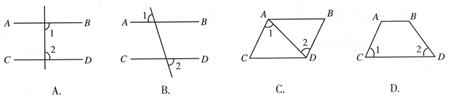
如图,在下列条件中,能判断AD∥BC的是
| A.∠DAC=∠BCA | B.∠DCB+∠ABC=180° | C.∠ABD=∠BDC | D.∠BAC=∠ACD |
A
解析试题分析:根据各选项中各角的关系及利用平行线的判定定理,分别分析判断AD、BC是否平行即可:
A、∵∠DAC=∠BCA,∴AD∥BC(内错角相等,两直线平行)。故本选项正确;
B、根据“∠DCB+∠ABC=180°”只能判定“DC∥AB”,而非AD∥BC.故本选项错误;
C、根据“∠ABD=∠BDC”只能判定“DC∥AB”,而非AD∥BC.故本选项错误;
D、根据“∠BAC=∠ACD”只能判定“DC∥AB”,而非AD∥BC.故本选项错误。
故选A。

练习册系列答案
相关题目
观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是()
| A.21 | B.28 | C.36 | D.45 |
如图,与∠1是同位角的是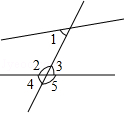
| A.∠2 | B.∠3 | C.∠4 | D.∠5 |
如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是
| A.40° | B.50° | C.60° | D.140° |
如图,甲顺着大半圆从A地到B地,乙顺着两个小半圆从A地到B地,设甲、乙走过的路程分别为a、b,则( )
| A.a="b" | B.a<b | C.a>b | D.不能确定 |
如图,下列条件中能判定直线l1∥l2的是【 】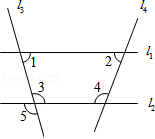
| A.∠1=∠2 | B.∠1=∠5 | C.∠1+∠3=180° | D.∠3=∠5 |