题目内容
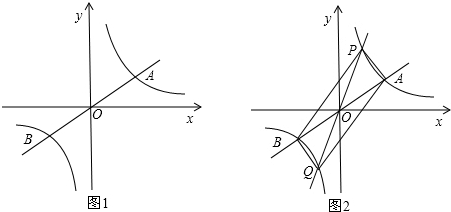
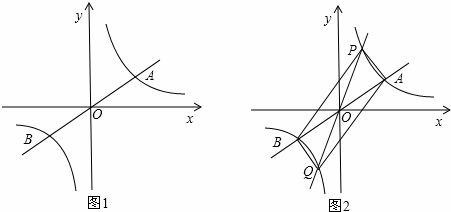
如图1,已知双曲线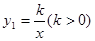 与直线
与直线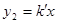 交于A,B两点,点A在第一象限.试解答下列问题:
交于A,B两点,点A在第一象限.试解答下列问题:
⑴若点A的坐标为(3,1),则点B的坐标为 ;
⑵当x满足: 时,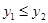 ;
;
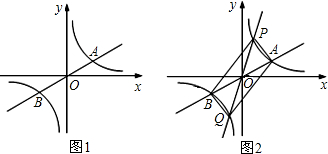
⑶过原点O作另一条直线l,交双曲线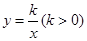 于P,Q两点,点P在第一象限, 如图2所示.
于P,Q两点,点P在第一象限, 如图2所示.
①四边形APBQ一定是 ;
② 若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积;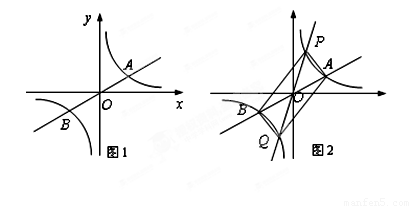
【答案】
(1)(-3,-1)(2)-3≤x<0或x≥3(3)①平行四边形②平行四边形APBQ的面积等于16
【解析】
试题分析:从图像可知该直线为正比例函数。所以则A为(3,1)则B为(-3,-1)
根据图像可判断-3≤x<0或x≥3时 。(3)由于直线PQ与直线AB都交于反比例函数上,可判断四边形对边两两平行且相等。为平行四边形。若A为(3,1)则反比例函数k=3.所以把P点横坐标x=1代入
。(3)由于直线PQ与直线AB都交于反比例函数上,可判断四边形对边两两平行且相等。为平行四边形。若A为(3,1)则反比例函数k=3.所以把P点横坐标x=1代入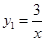 求出P坐标(1,3)。通过求出△BOP(由2个小三角形面积和)的面积等于4,而可证S△PAO=S△BOP(等底等高)得出平行四边形APBQ的面积等于16。
求出P坐标(1,3)。通过求出△BOP(由2个小三角形面积和)的面积等于4,而可证S△PAO=S△BOP(等底等高)得出平行四边形APBQ的面积等于16。
考点:反比例函数
点评:本题难度较大。主要考查学生结合反比例函数各知识点与平行四边形性质等的学习。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 与直线y=
与直线y=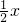 交于A,B两点,点A在第一象限,点A的横坐标为4.
交于A,B两点,点A在第一象限,点A的横坐标为4.
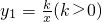 与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题:
与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题: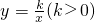 于P,Q两点,点P在第一象限,如图2所示.
于P,Q两点,点P在第一象限,如图2所示.