题目内容
 如图数轴上的点A、C分别表示-1和1,BC⊥AC且BC=1,以A为圆心,AB为半径作弧交数轴于点D,则点D表示的数是( )
如图数轴上的点A、C分别表示-1和1,BC⊥AC且BC=1,以A为圆心,AB为半径作弧交数轴于点D,则点D表示的数是( )分析:首先根据勾股定理求出AB长,再根据圆的半径相等可知AD=AB,再根据条件:点A、C分别表示-1和1,可求出D点坐标.
解答:解:∵BC⊥AC,
∴∠BCA=90°,
∴AB=
=
=
,
∵以A为圆心,AB为半径作弧交数轴于点D,
∴AD=AB=
,
∴点D表示的数是:
-1,
故选:C.
∴∠BCA=90°,
∴AB=
| AC2+CB2 |
| 4+1 |
| 5 |
∵以A为圆心,AB为半径作弧交数轴于点D,
∴AD=AB=
| 5 |
∴点D表示的数是:
| 5 |
故选:C.
点评:此题主要考查了勾股定理,以及数轴与实数,关键是求出AB的长.

练习册系列答案
相关题目
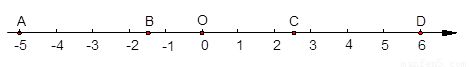
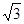 B、
B、 C、
C、
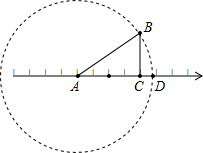 如图数轴上的点A、C分别表示-1和1,BC⊥AC且BC=1,以A为圆心,AB为半径作弧交数轴于点D,则点D表示的数是
如图数轴上的点A、C分别表示-1和1,BC⊥AC且BC=1,以A为圆心,AB为半径作弧交数轴于点D,则点D表示的数是


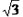
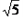
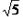 -1
-1 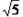 +1
+1